TP1 : La reprise

Note

Les objectifs du TP :

• Préparer votre environnement de travail et organiser votre dossier utilisateur.

• Réviser les bases de Python : Syntaxe, type, variables, branchements conditionnels, boucles et fonctions.

Environnement de travail

Dans Windows

Dans l’ordre :

1. Ouvrez votre session.

2. Dans votre répertoire créer un dossier nommé TP qui contiendra tous les TP de cette année.

3. Dans ce dossier, créer un dossier TP1 qui contiendra les fichiers de ce TP.

Dans l’IDLE

Lancez l’IDLE, Python 3. La fenêtre qui s’ouvre s’appelle “Python Shell” et ressemble peu ou prou à ça :

Note

Le symbole >>> s’appelle le “prompt” ou l”invite de commande”. Il signifie que l’interpréteur est disponible à prendre vos commandes.

Note

La syntaxe de base en Python :

• Les commentaires, que vous utiliserez (plus tard) pour annoter votre code afin de le rendre compréhensible et de vous souvenir de ce qu’il fait s’obtiennent avec un #.

  # Tout ce qui suit un dièse sur une ligne est ignoré
  

• De manière générale vous taperez une instruction par ligne, sans marqueur à la fin.

• Si vous souhaitez taper plusieurs instructions par ligne, il faudra les séparer par ;

• L’indentation est syntaxique et non décorative. Un bloc doit être indenté et doit toujours être précédé d’une ligne se terminant par un “:”

  if montant > 50:
      print("Frais de port offerts")
  else:
      print("Frais de port : 5 euros")
      montant += 5
  

Pyhton sait compter et il nous le prouve.

Exercice : Taper les différentes opérations suivantes (chacune sur une ligne) :

2 + 3; 3 - 5; -2 * 7; 9 ** 2; 3.11 / 2.7; 2.2 / 3.5; 15.0 / 2.0; 15 // 2; 16 % 3

Warning

On utilise la notation anglo-saxonne le point remplace la virgule.

Vous devriez obtenir quelque chose comme ça :

>>> 2 + 3
5
...

• Observez le format des différents résultats.

• Quittez l’IDLE et le relancer. Qu’observez-vous ?

Note

Opération	Résultat
+	Addition
-	Soustraction
*	Multiplication
**	Puissance
/	Division
//	Quotient dans la division euclidienne
%	Reste dans la division euclidienne

Warning

A la fermeture de l’IDLE tout ce qui est tapé dans le shell est perdu…

Note

Pour ouvrir/sauver un nouveau fichier vous pouvez utiliser le menu Edit ou Edition. Ou alors utiliser les raccourcis clavier : CTRL - N et CTRL - S.

De même pour l’exécuter vous pouvez utiliser le raccourci F5.

Exercice : Ouvrez une nouvelle fenêtre et sauvez le fichier dans votre dossier TP1 sous le nom : TP1.py. Dans ce fichier inscrivez les commandes suivantes :

1 + 1
print("2")
2 + 3
print(2 * 3)
2 * 3

Enregistrez et exécutez votre fichier. Qu’observez-vous ? Que fait Python exactement ?

Warning

Contrairement à ce qui se passe dans le shell, lorsqu’on exécute le code contenu dans un fichier Python effectue les calculs mais ne les affiche pas. Pour les afficher il faut le demander à l’aide de la commande print.

Exercice : Modifiez le code contenu dans le fichier TP1.py pour qu’à l’exécution il affiche la table de 7 après avoir fait les calculs.

Solution

print(1*7)
print(2*7)
print(3*7)
print(4*7)
print(5*7)
print(7*7)
print(8*7)
print(9*7)
print(10*7)

Exercice : Remplacez le code du fichier TP1.py par :

for i in range(1,11):
        print(i,"* 7 = ", i*7)

Enregistrez et exécutez le avec Python 3. Magique non ? Que signifie ce code d’après vous ?

Dans Spyder

Lancez Spyder. La fenêtre qui s’ouvre ressemble à ça :

Il y a trois panneaux qui constituent la fenêtre :

1. Une console IPython en bas à droite, prête à interpréter des commandes Python. Ici le prompt n’est pas le même car c’est une console IPython. Il prend la forme In [1]: avec un numéro d’entrée.

2. Un panneau d’information en haut à droite, qui comporte quatre onglets :

   • Un explorateur de variables.

   • Un explorateur de fichiers.

   • Une rubrique d’aide.

   • Un visualisateur de graphe.

3. Un éditeur à gauche dans lequel vous écrirez vos programmes.

Warning

Ne déplacez pas les différents panneaux !! Ne les redimensionnez pas non plus !!

Exercice : Vérifiez que la console réagit exactement comme le shell de l’IDLE, en exécutant quelques commandes.

Exercice : Ouvrez le fichier TP1.py et exécutez le.

Note

Dans Spyder aussi on peut utiliser des raccourcis clavier :

• CTRL-O : Ouvrir un fichier.

• CTRL-S : Sauvegarder.

• CTRL-N : Nouveau fichier.

• F5 : Exécuter.

Variables et Affectations

Littéraux

Note

Un littéral est une valeur écrite dans le programme.

Exemples :

• Un entier : 2

• Un nombre à virgule flottante : 3.14

• Un nombre complexe : 4j

• Une chaine de caractères : "PTSI-B"

• Une liste d’entiers : [3, 2, 1]

Lorsque vous tapez un littéral dans la console Python crée, disons, un nouvel “objet”.

>>> (2022, id(2022), type(2022))
(2020, 4342639664, <class 'int'>)

En plus de sa valeur, Python assigne à l’objet un identifiant, ici 4342639664, qui indique où l’objet est gardé en mémoire et un type, ici int pour entier.

Nous verrons plus en détail les types un peu plus loin, parmi les principaux on trouve :

• Les entiers int

• Les flottants float

• Les chaines de caractères str

• Les listes list

• Les booléens bool

• Les dictionnaires dict

Variables et affectations

L’identifiant d’un objet est assez contraignant à utiliser. On a alors recourt aux variables.

Note

Une variable permet de stocker en mémoire une donnée pour la réutiliser à plusieurs reprises en la désignant par un nom.

Pour donner une valeur à une variable en Python on utilise le symbole = , cette opération s’appelle une affectation de valeur à une variable, ou plus simplement une affectation de variable.

Une affectation crée une liaison entre un nom et une donnée stockée en mémoire.

Warning

Les noms de variable (et aussi : de fonction, de classe…) doivent respecter certaines règles syntaxiques :

• Ils ne peuvent contenir que des lettres, des chiffres, des underscores ( _ ), et doivent commencer par une lettre.

• La casse est importante, autrement Python fait la différence entre majuscule et minuscule (ma_variable ≠ Ma_VaRiAbLE).

• D’après la PEP8, les noms de variables doivent être écrits en minuscules, avec des underscores si nécessaire : ma_variable.

• Les noms des constantes doivent être écrits tout en majuscules, avec des underscores si nécessaire : UNE_CONSTANTE.

• Certains noms sont réservés par le langage et ne peuvent être utilisés comme nom de variable. Voici la liste pour Python 3 :

  and	assert	break	class	continue
  def	del	elif	else	except
  exec	finally	for	from	global
  if	import	in	is	lambda
  not	or	pass	print	raise
  return	try	while	yield	as
  with

Dans un programme complexe, il faut impérativement donner des noms significatifs aux variables, de sorte d’en faciciliter la lecture et la compréhension.

Warning

Le symbole = utilisé pour l’affectation ne représente pas une égalité. En particulier il n’est pas symétrique.

In [1]: a = 2

In [2]: a
Out[2]: 2

In [3]: 2 = a
  Input In [3]
    2 = a
    ^
SyntaxError: cannot assign to literal

Note

Il est d’usage de laisser une espace avant et une autre après le signe =.

Exercice : Dans la console créez une variable mon_annee et affectez lui votre année de naissance. Demandez à Python son identifiant et son type à l’aide des commandes id() et type(). Taper ensuite les différentes commandes suivantes :

mon_annee + 1 ; 3*mon_annee ; mon_annee + mon_annee ;

Exercice : Dans la console tapez les lignes suivantes.

In [4]: a = 3

In [5]: a = a + 2

Que vaut a à votre avis ? Vérifiez en affichant la valeur de a.

In [6]: a += 2

In [7]: a
Out[7]: 7

Qu’a fait Python ? Essayez avec d’autres valeurs que 2 et avec d’autres opérateurs que +.

Solution

Il est équivalent de taper a += 2 ou de taper a = a + 2.

Note

On peut abréger certaines affectations.

a -= k
a /= k
a //= k
a %= k
a *= k
a **= k

Exercice : Dans la console, tapez les commandes suivantes.

In [8]: a = 10

In [9]: b = 20

In [10]: a = b

In [11]: b = a

Que valent a et b maintenant ? Vérifiez.

Solution

a = 20 et b = 20.

Essayez les commandes suivantes :

In [12]: a = 10

In [13]: b = 20

In [14]: c = a

In [15]: a = b

In [16]: b = c

Que valent a et b maintenant ? Vérifiez.

Solution

a = 20 et b = 10. On a échangé les valeurs de a et de b.

Observez ce qu’il se passe s’il on fait :

In [17]: a = 10

In [18]: b = 20

In [19]: print("a = ", a, "b = ", b)
a =  10 b =  20

In [20]: (a,b) = (b,a)

In [21]: print("a = ", a, "b = ", b)
a =  20 b =  10

Que s’est-il passé ?

Note

On parle d’affectations multiples lorsqu’on affecte plusieurs variables en même temps. Par exemple :

In [22]: (a, b) = (4, 5) ; (a, b)
Out[22]: (4, 5)

In [23]: (a, b) = (b, a) ; (a, b)
Out[23]: (5, 4)

C’est très pratique pour échanger les valeurs de deux variables.

Exercice : Copiez-collez les instructions suivantes dans le fichier TP1.py et sauvez.

a = 10
b = 20
c = 30
a *= 2
c = b-a
print((a+b)*c+1)

Quel résultat va s’afficher à l’exécution ? Vérifiez.

Solution

1

Types de données simples

Note

En Python le typage des données est dynamique : les variables n’ont pas à proprement parler de type, c’est leurs valeurs qui en ont un. Donc au cours de l’exécution une même variable peut contenir des valeurs de types différents.

In [24]: a = 4

In [25]: type(a)
Out[25]: int

In [26]: a = (3, 8)

In [27]: type(a)
Out[27]: tuple

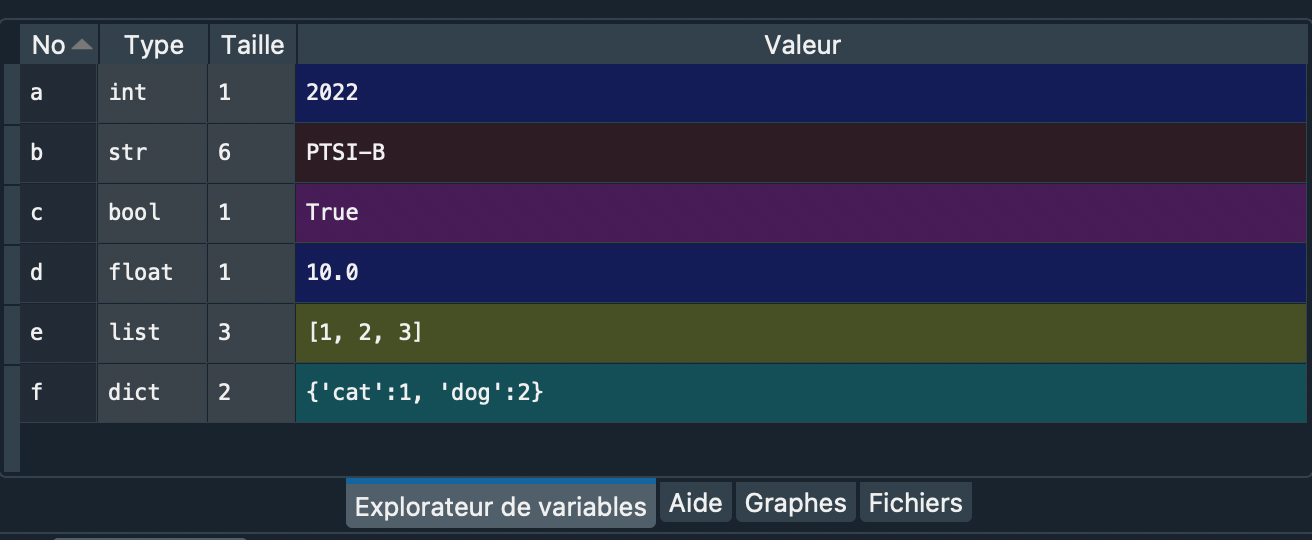
Dans Spyder vous pouvez utilisez l’explorateur de variables pour connaître la valeur et le type d’une variable, et l’espace mémoire qui lui est alloué.

In [28]: a = 2

In [29]: b = 'PTSI-B'

In [30]: c = True

In [31]: d = 10.

In [32]: e = [1, 2, 3]

In [33]: f = {'cat': 1, 'dog': 2}

Ce qui donnera :

Les nombres

En Python il y a essentiellement quatre types de nombres :

• Les entiers de type int

• Les flottants de type float

• Les complexes de type complex

• Les fractions de type fraction

Exercice : Qu’observez-vous quant aux types dans les résultats suivants ?

In [34]: a = 1 ; type(a)
Out[34]: int

In [35]: b = 1. ; type(b)
Out[35]: float

In [36]: import cmath

In [37]: c = 1j ; type( c )
Out[37]: complex

In [38]: import fractions

In [39]: d = fractions.Fraction(3,8) ; f = fractions.Fraction(6,4)

In [40]: print(d+f); type(d)
15/8
Out[40]: fractions.Fraction

In [41]: a+2 ; type(a+2)
Out[41]: int

In [42]: 2*a ;type(2*a)
Out[42]: int

In [43]: a+2. ; type(a+2.)
Out[43]: float

In [44]: 2.*a ; type(2.*a)
Out[44]: float

In [45]: b+2 ; type(b+2)
Out[45]: float

In [46]: b+2. ; type(b+2.)
Out[46]: float

In [47]: 2 + c ; type(2+c)
Out[47]: complex

Note

Python applique lui-même des conversions de types, on dit que ces conversions sont implicites.

Le conversions de type numérique int → float → complex sont les seules conversions implicites de type qui sont autorisées, toutes les autres sont formellement interdites et aboutissent à un message d’erreur. C’est pourquoi on dit que le typage est fort.

Lien vers la documentation du module de math

Exercice : Que pouvez-vous déduire des résultats suivants ?

In [48]: 2 ** 100
Out[48]: 1267650600228229401496703205376

In [49]: 2. ** 100
Out[49]: 1.2676506002282294e+30

Solution

On peut en déduire que le type int est plus précis que le type float.

Note

Lorsque l’on veut modeliser un problème il faut choisir entre les types int et float pour représenter une donnee numerique.

• Si la valeur exacte des calculs est importante les entiers sont plus appropries, de même si les calculs portent sur des donnees d’ordres de grandeur très differents.

• Les flottants sont utiles pour repr ́esenter des grandeurs physiques par exemple comme la vitesse, la temperature, le temps, etc…, dont seuls les premiers chiffres sont significatifs.

Chaînes de caractères

Note

Une chaine de caractères, comme son nom l’indique est une série de lettres.

On peut écrire une chaine de caractère de plusieurs façons :

• entre guillemets

• entre apostrophes

• entre triples guillemets

Le type d’une chaine est str.

In [50]: s1 = "Bonjour "

In [51]: s2 = ' à '

In [52]: s3 = """ tous."""

In [53]: type(s1)
Out[53]: str

On peut concaténer des chaines de caractère à l’aide de l’opérateur + et les répéter à l’aide de *.

In [54]: print(s1+s2+s3)
Bonjour  à  tous.

In [55]: print(2*s1)
Bonjour Bonjour 

On peut accéder aux différentes lettres d’une chaine de caractère en utilisant des crochets [].

Exercice : Observez les résultats ci-dessous, et en déduire le sens de s[p:q:r].

In [56]: s = "Hello World!"

In [57]: print(s)
Hello World!

In [58]: s[0]
Out[58]: 'H'

In [59]: s[11]
Out[59]: '!'

In [60]: s[3:5]
Out[60]: 'lo'

In [61]: s[:5]
Out[61]: 'Hello'

In [62]: s[6:]
Out[62]: 'World!'

In [63]: s[:]
Out[63]: 'Hello World!'

In [64]: s[-3]
Out[64]: 'l'

In [65]: s[-3:]
Out[65]: 'ld!'

In [66]: s[0:8:2]
Out[66]: 'HloW'

In [67]: s[::3]
Out[67]: 'HlWl'

Solution

s[p:q:r] retourne la chaine de caractères formée par les caractères de la chaine s d’indice \(i\) tels que \(p\leq i< q\) avec un pas de \(r\). Si l’on omet le premier ou le dernier indice on considère que respectivement l’on commence à \(0\), ou que l’on va jusqu’au bout de la chaine. A noter que le pas est optionnel.

Exercice : Définissez la chaine de caractère s = "0123456789" et écrivez les instructions qui afficheront les résultats suivants :

'0123456789'
'5'
'345'
'789'
'02468'
'13579'
'036'

Solution

In [68]: s = '0123456789'

In [69]: s
Out[69]: '0123456789'

In [70]: s[5]
Out[70]: '5'

In [71]: s[3:6]
Out[71]: '345'

In [72]: s[7:]
Out[72]: '789'

In [73]: s[::2]
Out[73]: '02468'

In [74]: s[1::2]
Out[74]: '13579'

In [75]: s[:7:3]
Out[75]: '036'

Note

Une liste de commande pour obtenir certains caractères ou pour formater du texte.

Utilité	Caractère
Aller à la ligne	\n
Tabulation	\t
Afficher un anti-slash	\
Afficher une apostrophe	\’
Afficher un guillemet	\”
Saut de page	\f
Retour en arrière	\b
Retour chariot	\r

Exercice : Dans la console tapez les instructions qui affichent (en respectant la mise en forme exacte) :

"J'aime beaucoup Python.
        Même si je ne comprends pas tout."

Solution

In [76]: s = "\"J\'aime beaucoup Python.\n \t Même si je ne comprends pas tout.\""

Note

Les chaines de caractères sont non-mutables !

In [77]: s = 'abcdef'

In [78]: s[1] = a
---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
Input In [78], in <cell line: 1>()
----> 1 s[1] = a

TypeError: 'str' object does not support item assignment

Les booléens

Note

En Python les booléens vrai et faux se notent True, False.

Ils sont manipulables avec les opérations standards +, -, *, \, or, and, not et avec les opérateurs de comparaison.

Les opérateurs de comparaison sont :

• L’égalité ==

• L’inégalité !=

• Les comparateurs d’ordre : < <= > >=

• L’identité is qui compare les id() .

Ils retournent un booléen.

L’évaluation d’une expression booléenne s’arrête dès que le résultat est connu (opérateurs paresseux ou en court-circuit)

In [79]: True and False
Out[79]: False

# Les expressions a et b ne sont pas évaluées
In [80]: a = True; b = False; True and (a or b)
Out[80]: True

In [81]: not False
Out[81]: True

Exercice : Tapez dans la console et évaluez les instructions suivantes.

True + True ; True + False ; True * False ; False + False ; False * False
2 < 3
2 != 3
s1 = "trois" ; s2 = "sept"
s1 > s2
2 + 3 == 5
a = 2 ; b = 2.
a == b
a is b
a = 2 ; b = 2
a == b
a is b
1 < 2 and 3 <= 5
not(3 > 4)
'a'+'b' == 'ab' or 7 < 3

Solution

In [82]: True + True
Out[82]: 2

In [83]: True + False
Out[83]: 1

In [84]: True * False
Out[84]: 0

In [85]: False + False
Out[85]: 0

In [86]: False * False
Out[86]: 0

In [87]: 2 < 3
Out[87]: True

In [88]: 2 != 3
Out[88]: True

In [89]: s1 = "trois" ; s2 = "sept"

# Ici c'est l'ordre lexicographique
In [90]: s1 > s2
Out[90]: True

In [91]: 2 + 3 == 5
Out[91]: True

In [92]: a = 2 ; b = 2.

In [93]: a == b
Out[93]: True

In [94]: a is b
Out[94]: False

In [95]: a = 2 ; b = 2

In [96]: a == b
Out[96]: True

In [97]: a is b
Out[97]: True

In [98]: 1 < 2 and 3 <= 5
Out[98]: True

In [99]: not(3 > 4)
Out[99]: True

In [100]: 'a'+'b' == 'ab' or 7 < 3
Out[100]: True

Conversion de types

Note

En Python on peut faire certaines conversions de type, pour transformer un nombre en chaine de caractère ou l’inverse par exemple.

In [101]: s = str(123) ; print(s) ; type(s)
123
Out[101]: str

In [102]: s = int(s) ; print(s) ; type(s)
123
Out[102]: int

Exercice : Dans la console essayez les conversions suivantes :

float(123) ; bool(0) ; str(True) ; float(’1.22’) ; int(1.23)
bool(1) ; bool(’abc’) ; float(’123’) ; int(True) ; str(123) ; bool(’’)
float(True) ; int(False) ; str(1.23) ; bool(1.23) ; float(False)

Entrées-sorties

Note

Pour afficher un résultat dans la console on utilise la commande print

In [103]: a = 3

In [104]: b = 2

In [105]: print("La somme de {} et {} est {}".format(a,b,a+b))
La somme de 3 et 2 est 5

La méthode de chaine de caractères format permet de formater une chaine avec des expressions. On peut aussi utiliser les f-string pour faire la même chose. Une f-string est une chaine de caractères préfixée par f ou F :

In [106]: a = 3

In [107]: b = 2

In [108]: print(f"Le produit de {a} et {b} est {a*b}")
Le produit de 3 et 2 est 6

La fonction print est très pratique pour afficher des résultats intermédiaires lorsque l’on cherche à déboguer un programme. Bien entendu Python offre mieux pour le logging.

Pour lire une entrée au clavier on utilise la commande input en Python 3 le résultat est un chaine de caractère.

n = int(input("Entrez un nombre : ")) ; print(n/2)

Pour en savoir plus sur les entrées-sorties c’est par ici.

Exercice : Ecrire dans un fichier un programme qui demande à l’utilisateur son nom, son prénom et son année de naissance et qui retourne le résultat suivant sous la forme :

Nom : Leponge
Prénom : Bob
Année de naissance : 1900

Solution

nom = input("Entrez votre nom : ")
prenom = input("Entrez votre prénom : ")
annee = input("Entrez votre année de naissance : ")
print("Nom : {}\rPrénom : {} \rAnnée de naissance : {}".format(nom,prenom,annee))

Exercice : Ecrire dans un fichier un programme qui demande à l’utilisateur le rayon d’une sphère et qui retourne le résultat suivant sous la forme :

Entrez le rayon en cm : 5
Une sphere de rayon 5.0 cm a pour surface : 314.159265359 cm2
Une boule de rayon 5.0 cm a pour volume : 523.5987755982989 cm3

Solution

from math import pi
rayon = float(input("Entrez le rayon en cm : "))
s = 4*pi*rayon**2
v = 4/3*pi*rayon**3
print(f"Une sphere de rayon {rayon} cm a pour surface : {s} cm2.")
print(f"Une boule de rayon {rayon} cm a pour volume : {v} cm3.")

Exercice : Ecrire dans un fichier un programme qui demande à l’utilisateur son nom et son prénom et qui retourne ses initiales.

Solution

nom = input("Entrez votre nom : ")
prenom = input("Entrez votre prenom : ")
print("Vos initiales sont  : {}.{}.".format(nom[0],prenom[0]))

Structures de contrôle

Instruction conditionnelle

Note

Les instructions conditionnelles sont essentielles en informatique. Elles permettent d’exécuter des instructions sous réserve que certaines soient vérifiées.

Un exemple très simple, dans le quel on test si la valeur d’une variable est plus petite que 3, et si c’est le cas on affiche qu’elle l’est.

>>> if a < 3 :
...     print("a est plus petit que 3")

Cette structure de condition est dite minimale. Il en existe des plus complexes.

Warning

L’indentation est essentielle ! L’indentation c’est le décalage marqué sur la seconde ligne. Il est égal à 4 espaces (c’est mieux) ou une tabulation. On ne mélange pas les espaces et les tabulations !

Note

Une structure conditionnelle complète suit le schéma suivant :

if condition_1:
        instructions_1

elif condition_2:
        instructions_2

elif condition_3:
        instructions_3
...

else:
       instructions_else

Les instructions de la première condition évaluée à True sont exécutées, si aucune ne l’est on exécute instructions_else .

Exercice : Si x, y et z sont des nombres, quelle est la valeur de m à la fin de cet algorithme ?:

m   =   0
if x > y:
    if x > z:
        m   =   x
    else:
        m   =   z
else:
    if y > z:
        m   =   y
    else:
        m   =   z

Vérifiez le.

Exercice : Ecrire un programme qui prend comme entrée un entier n et qui affiche le double s’il est impair, le triple s’il est pair mais pas divisible par 4 et sa moitié sinon.

Solution

if n % 2 == 1:
    print(2*n)
elif n % 4 ==0:
    print(n//2)
else:
    print(3*n)

Exercice : Ecrire un programme qui demande les trois coefficients réels d’un trinôme \(ax^2+bx+c\) à l’utilisateur et qui retourne une phrase indiquant le nombre de racines réelles distinctes de ce trinôme, après avoir vérifié qu’il s’agissait bien d’un polynôme du second degré.

Solution

a = float(input("Entrez le coefficient a : "))
b = float(input("Entrez le coefficient b : "))
c = float(input("Entrez le coefficient c : "))
if a == 0:
    print("Ce n'est pas un polynôme de degré deux !")
else:
    delta = b**2 - 4*a*c
    if delta > 0:
        print("Le trinôme {}*x^2+{}*x+{} possède deux racines réelles distinctes.".format(a,b,c))
    elif delta == 0:
        print("Le trinôme {}*x^2+{}*x+{} possède une racine réelle.".format(a,b,c))
    else:
        print("Le trinôme {}*x^2+{}*x+{} ne possède pas de racines réelles.".format(a,b,c))

Exercice : Ecrire un programme qui demande une année à l’utilisateur et qui indique si elle est bissextile ou non. Une année est bissextile par définition si sa valeur vérifie l’une des conditions :

• être multiple de 4 mais pas de 100 ;

• être multiple de 400.

Solution

annee = int(input("Entrez une année : "))
if annee % 4 != 0:
    print("L'année {} n'est pas bissextile".format(annee)})
elif annee % 100 != 0:
    print("L'année {} est bissextile".format(annee)})
elif annee % 400 != 0:
    print("L'année {} n'est pas bissextile".format(annee)})
else:
    print("L'année {} est bissextile".format(annee)})

Solution 2 : avec les mots or et and

annee = input("Saisissez une année : ") # L'utilisateur fournit une année à tester
annee = int(annee) # Erreur si l'utilisateur n'a pas saisi un nombre

if annee % 400 == 0 or (annee % 4 == 0 and annee % 100 != 0):
    print("L'année saisie est bissextile.")
else:
    print("L'année saisie n'est pas bissextile.")

Petit problème : Ecrire un programme qui retourne le plus grand nombre parmi les quatre nombres w, x, y et z.

Solution 2 : avec les mots or et and

maximum = w
if x > w:
      maximum = x
      if y > x or y > z:
            maximum = y
      elif z > x:
            maximum = z
else:
      if y > w or y > z:
            maximum = y
      elif z > w:
            maximum = z
return maximum

Boucle while

Note

Les boucles permettent de répéter certaines opérations autant de fois que nécessaire. Nous en verrons de deux sortes.

Une boucle while permet de répéter un bloc d’instructions tant qu’une condition est vérifiée. La structure d’une boucle while (tant que en anglais) est la suivante :

while condition: # Tant que la condition est remplie effectuer les instructions
        instructions

Un exemple : La table de 7.

i = 0 # On initialise notre compteur
while i < 10: # Tant que le compteur i est strictement plus petit que 10 faire :
        print("{} * 7 = {}".format(i+1,(i+1)*7)) # Afficher le résultat
        i += 1 # Incrémenter le compteur

Warning

Si dans ce programme vous oubliez d’incrémenter le compteur il ne sera jamais supérieur ou égale à 10 et votre programme ne s’arrêtera jamais !! On appelle ça une boucle infinie. Si vous avez lancé une boucle infinie vous pouvez l’arrêter avec CTRL - C si vous êtes dans un shell ou à l’aide du bouton triangulaire orange dans la console de Syder.

Exercice : Ecrire un programme qui calcule la somme des \(100\) premiers entiers.

Solution

somme = 0 #Initialisation de la somme
i=0 #Initialisation du compteur
while i <= 100: #Tant que i est plus petit que 20 faire
    somme += i #Ajouter i à somme
    i += 1 #Incrémenter i de 1

Exercice : Que vaut somme à la fin ?

somme = 0
i=0
while i <= 20:
        if i % 2 == 0:
                somme += i
        i += 1

Réécrire ce code sans la structure conditionnelle.

Solution

somme contient la somme des nombres pairs de \(0\) à \(20\).

somme = 0 #Initialisation de la somme
i=0 #Initialisation du compteur
while i <= 20: #Tant que i est plus petit que 20 faire
    somme += i #Ajouter i à somme
    i += 2 #Incrémenter i de 2

Exercice : (Racine carrée entière) Ecrire un programme qui demande à l’utilisateur un nombre entier n , qui affiche l’entier dont le carré est l’entier, inférieur ou égal, le plus proche de n. Par exemple il affichera 2 si l’utilisateur rentre 7.

Solution

n = int(input("Entrez un entier : "))
i = 0 # Initialisation du compteur
while (i+1) ** 2 <= n: #Tant que le carré du compteur i est plus petit que n faire
   i += 1 # Incrémenter i
print(" La racine carrée entière de {} est : {}".format(n, i)

Exercice : Ecrire un programme qui calcule la somme des multiples de 3 ou de 5 strictement inférieurs à 1000.

Solution

In [109]: i=0

In [110]: somme = 0

In [111]: while i < 1000:
   .....:     if i % 3 == 0 or i % 5 == 0:
   .....:         somme += i
   .....:     i += 1
   .....: 

In [112]: somme
Out[112]: 233168

Exercice : (L’algorithme des différences successives)

Que calcule cet algorithhme ? Le modifier pour obtenir la division euclidienne de a par b.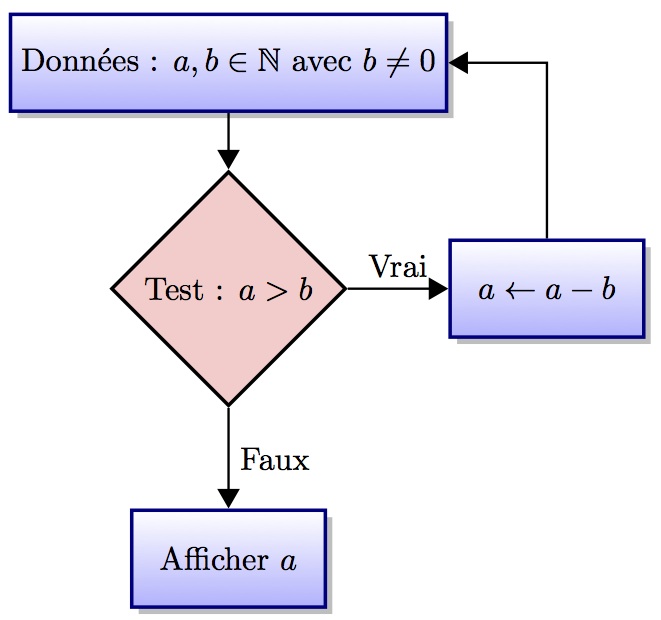

Solution

q = 0
r = a
while b < r:
    q += 1
    r -= b

Petit problème 1 :

On définit la suite de Fibonacci par :

Calculer la somme des termes pairs plus petit que quatre millions.

Solution

In [113]: a = 1

In [114]: b = 2

In [115]: somme = b

In [116]: while b <= 4*10**6:
   .....:       a, b = b, a + b
   .....:       if b % 2 == 0:
   .....:             somme += b
   .....: 

In [117]: somme
Out[117]: 4613732

Boucle for

Note

La structure d’une boucle for (pour en anglais) est la suivante :

for element in iterable: # Pour tous les éléments de l'itérable faire :
        instructions

La boucle for permet d’effectuer un bloc d’instructions pendant que element prend successivement toutes les valeurs dans itérable .

Un exemple : Avec une chaine de caractères comme itérable.

chaine = "Vive la PTSI-B!"
for lettre in chaine: # Pour chaque lettre dans chaine faire :
        print(lettre) # Afficher la lettre

Notez bien que c’est la commande for qui a crée le variable lettre.

Exercice : Dans la console écrire un programme qui affiche toutes les consonnes de la chaine “Vive les TP Python en PTSI-B” et qui affiche un underscore à la place des voyelles.

Solution

chaine = "Vive les TP Python en PTSI-B"
for lettre in chaine:
    if lettre not in "AEIOUYaeiouy":
        print(lettre)
    else:
        print("_")

Note

La fonction range est très utile, elle génère des itérables constitués par des suites de nombres, on l’utilise comme suit :

range(m) # Ensemble des entiers de :math:`0` à :math:`m-1`
range(n, m) # Ensemble des entiers de :math:`n` à :math:`m-1`
range(n, m, p) # Ensemble des entiers de :math:`n` à :math:`m-1` par pas de :math:`p`

Exercice : Dans la console écrire un programme qui affiche la somme des carrés des entiers de 10 à 38, puis la somme des cubes des entiers impaires de 10 à 38, qui utilise l’expression range().

Solution

In [118]: somme = 0

In [119]: for i in range(10,39):
   .....:     somme += i**2
   .....: 

In [120]: somme
Out[120]: 18734

In [121]: somme2 = 0

In [122]: for i in range(11,15,2):
   .....:     somme2 += i**3
   .....: 

In [123]: somme2
Out[123]: 3528

Exercice : Dans la console écrire un programme qui calcule \(5^{245}\) en effectuant toutes les multiplications. Comparer avec 5**245.

Solution

In [124]: resultat = 5

In [125]: for _ in range(1, 245):
   .....:     resultat *= 5
   .....: 

In [126]: resultat
Out[126]: 1768687320083342259279124861501521832164556874636550427652854470690527601287665061472564736711124628799600085800171451104664596264311182682860135173541493713855743408203125

Exercice : Dans la console écrire un programme qui calcule \(50!\) en effectuant toutes les multiplications. Comparer le résultat avec la fonction factorial du module math. Calculer la somme des décimales de ce nombre.

Solution

In [127]: resultat = 1

In [128]: for i in range(2,51):
   .....:     resultat *= i
   .....: 

In [129]: resultat
Out[129]: 30414093201713378043612608166064768844377641568960512000000000000

# Première méthode
In [130]: somme = 0

In [131]: n = resultat

In [132]: while n > 0:
   .....:     somme += (n % 10)
   .....:     n = n // 10
   .....: 

In [133]: print("La somme des décimales est : {}".format(somme))
La somme des décimales est : 216

# Seconde méthode
In [134]: somme2 = 0

In [135]: chaine = str(resultat)

In [136]: for chiffre in chaine: somme2 += int(chiffre)

In [137]: somme2
Out[137]: 216

Les fonctions

Définition et appels

Note

Une fonction permet d’appeler un groupe d’instructions à plusieurs reprises, sans avoir à le réécrire. Vous connaissez déjà un certain nombre de fonctions comme print, input ou encore range.

En Python une fonction se déclare à l’aide du mot-clé def.

Par exemple :

def ma_fonction(arg_1,...,arg_n):
    instruction 1
    ...           #Les instructions forment le **corps** de la fonction.
    instruction p

Observons ce qui se passe en tapant :

In [138]: def double(x):
   .....:     print(2*x)
   .....: double(5)
   .....: 
10

Dans cet exemple la fonction double prend un argument, ici appelé x. Cet argument n’a pas de type à priori. On peut essayer avec différents type de donnée pour x . Comme par exemple :

In [139]: double(5)
10

In [140]: double(5.)
10.0

In [141]: double("x")
xx

Taper les commandes suivantes dans la console.

In [142]: def double_bis(x):
   .....:      return 2*x
   .....: 

In [143]: double_bis(2)
Out[143]: 4

In [144]: n = double_bis(2)

In [145]: n # On a affecté la valeur retournée par la fonction à n
Out[145]: 4

In [146]: m = double(2)
4

In [147]: m

In [148]: print(m) # Il n'y a rien dans m
None

Qu’elle est la différence ?

La fonction double affiche le résultat, la fonction double_bis retourne une valeur. Pour renvoyez un résultat il faut utiliser le mot-clé return.

On peut noter que la console IPython fait bien la différence.

Danger

Ne confondez surtout pas afficher et retourner, ou return et print.

Si vous oubliez le mot-clé return, il ne se passera rien, ou plutôt votre fonction renverra None.

>>> def double_ter(x):
...     2*x
...
>>> double_ter(2)
>>> print(double_ter(2))
None
>>>

En informatique, une fonction qui ne retourne rien s’appelle une procédure.

Note

D’après la PEP8, les noms de fonctions doivent être écrits en minuscules, avec des underscores si nécessaire.

De bonnes pratiques !

Lorsque l’on définit une fonction, il est impératif de l’accompagner d’une docstring, c’est-à-dire d’une description de ce que fait la fonction, des arguments qu’elle prend et de ce qu’elle retourne le cas échéant (on ajoute aussi les exceptions qu’elle peut soulever mais nous verrons ça plus tard). Une dernière chose : il est d’usage d’écrire cette docstring en anglais… La PEP-257 décrit la bonne manière d’écrire une docstring en python, mais je préfère suivre les conseils donnés dans le guide Google. Voici un exemple de docstring :

def square_root(x):
    """
    Calculate the square root of a number.

    Args:
        x : the positive positive number to get the square root of.
    Returns:
        the square root of x.
    Raises:
        TypeError: if x is not a number.
        ValueError: if x is negative.
    """

Vous devez écrire une docstring pour chaque fonction que vous définirez !

Pour aller plus loin encore, on peut utiliser les annotations de fonctions, ou typing. Il s’agit de spécifier le type des arguments passés à la fonction et de spécifier le type de ce que la fonction retourne le cas échéant de la manière suivante :

def ma_fonction(arg_1:type_1,...,arg_n:type_n)->type_sortie:

Par exemple pour la fonction square_root on aurait :

def square_root(x:float)->float:

Notez que ce ne sont que des indications, Python ne vérifie rien et ne dira rien si vous ne respectez pas vos propres définitions. Pour en savoir plus c’est par ici.

Exercice : Ecrire une fonction somme_n_entiers qui prend comme argument un entier n et qui retourne la somme des \(n\) premiers entiers.

Solution

def somme_n_entiers(n:int)->int:
    """
    Calculate the sum of the n firsts integers

    Args:
        n : the last integer of the sum.
    Returns:
        1 + ... + n.
    """
    s = 0
    for i in range(n+1):
        s += i
    return s

Exercice : Ecrire une fonction percentage qui prend deux nombres comme arguments score et total et qui retourne le pourcentage de réussite que représente score.

Solution

def percentage(total:float, score:float)->float:
    """
    calculate the percentage corresponding to a grade.

    Args:
        total : a postive number > 0
        score : a number 0 <= score <= total

    Returns:
        the percentage corresponding to the score obtained.
    """
    return 100*score/total

Note

Lorsque l’on écrit une fonction, on peut vouloir vérifier que des conditions qui sont censées être satisfaites le sont effectivement, à l’aide du mécanisme d’assertion proposé par Python.

Par exemple, voici comment utiliser la fonction assert pour vérifier que les préconditions de la fonction percentage sont bien vérifiées :

def percentage(total:float, score:float)->float:
    """
    calculate the percentage corresponding to a grade.

    Args:
        total : a postive number > 0
        score : a number 0 <= score <= total

    Returns:
        the percentage corresponding to the score obtained.
    """
    assert type(score) == float, "score must be a float number."
    assert type(total) == float, "total must be a float number."
    assert total > 0, "total must be strictly positive"
    assert score >= 0, "score must be positive."
    assert total >= score, "score must be smaller than total."
    return 100*score/total

Copiez-collez ce code et essayez le avec des préconditions non respectées, vous verrez que l’exécution du code s’interrompt avec la levée d’une exceprion de type AssertionError, et que le message d’erreur prévu s’affiche, ce que nous n’aurions pas obtenu en utilisant des if.

Dans la vraie vie, on n’’utilise des assertions qu’en phase de développement jamais en production, à moins que la fonction soit interne à un module, donc votre code doit fonctionner même si on les supprime.

Exercice : Ecrire une fonction factorielle qui prend comme argument un entier n et qui retourne \(n!\), après avoir testé que \(n\) est bien un entier positif.

Solution

def factorielle(n:int)->int:
    """
    Calculate the factorial of n

    Args:
        n : the positive integer to get the factorial
    Returns:
        1 x ... x n.
    """
    assert type(n) == int, "n must be an integer."
    assert n >= 0, "n must be positive"
    f = 1
    for i in range(1, n+1):
        f *= i
    return f

Exercice : Ecrire une fonction syracuse1 qui prend comme argument un entier N positif et qui retourne \(u_{100}\) où la suite \((u_k)_{k\in\mathbb{N}}\) est définie par \(u_0 = N\) et pour tout \(k\in\mathbb{N}\), \(u_{k+1} = u_k / 2\) si \(u_k\) est pair et sinon \(u_{k+1}=3 u_k + 1\). Vous testerez que :code:`N`est bien un entier positif.

Solution

def syracuse1(N:int)->int:
    """
    Calculate the hundredth term of the syracuse sequence of N

    Args:
        N : the integer u_0 > 0
    Returns:
        u_100
    """
    assert type(N) == int, "N must be an integer."
    assert N >=0, "N must be positive."
    u = N
    for _ in range(100):
        if u % 2 == 0:
            u = u // 2
        else:
            u = 3*u+1
    return u

Exercice : Ecrire une fonction fibo qui prend comme argument un entier n et qui retourne le n-ième terme de la suite de Fibonacci. Après avoir testé que :code:`n`est bien un entier positif.

Solution

def fibo(n:int)->int:
    """
    Calculate the n-th term of the Fibonacci sequence.

    Args:
        n : a positive integer
    Returns:
        u_n
    """
    assert type(n) == int, "n must be an integer."
    assert n >= 0, "n must be positive."
    u = 1
    v = 2
    for _ in range(n):
        u, v = v, u+v
    return u

Exercice : Ecrire une fonction is_positive qui prend comme argument un réel x est qui renvoie True si x est positif et False sinon. Après avoir testé que x est bien un nombre flottant.

Solution

def is_positive(x:float)->bool:
    """
    Test if x is positive

    Args:
        x : the number to determine is positive or not.
    Returns:
        True if x is positive, and False otherwise.
    """
    assert type(x) == float, "x must be a float number."
    return x >= 0

Exercice : Ecrire une fonction somme_dec qui prend comme argument un entier n positif et qui retourne la somme de ses décimales. Après avoir testé un que n est un entier.

Solution

def somme_dec(n:int)->int:
    """
    Calculate the sum of the digits of n.

    Args:
        n : the number of which we will calculate the sum of the digits.
    Returns:
        The sum of the digits of n
    """
    assert type(n) == int, "n must be an integer."
    assert n >= 0, "n must be positive."
    s = 0
    while n > 0:
        s += n % 10
        n //= 10
    return s

Exercice : Ecrire une fonction is_palindrome qui prend comme argument une chaine de caractères et qui retourne True si cette chaine est un palindrome et False sinon. Après avoir testé que :code:`chaine`est bien une chaine de caractères de longueur supérieure ou égale à deux.

Solution

def is_palindrome(chaine:str)->bool:
    """
    Test if a string is a palindrome.

    Args:
        chaine : a string to test.
    Returns:
        True if chain is a palindrome, and False otherwise.
    """
    assert type(chaine) == str, "type(chaine) must be str."
    assert len(chaine) >= 2, "len(chaine) must be greater than 2."
    i = 0
    res = True
    while res and i < len(chaine)//2:
        if chaine[i] != chaine[-(i+1)]:
            res = False
        i += 1
    return res

Note

Une fonction peut renvoyer des données de tout type.

Arguments

Note

Une fonction peut ne pas prendre d’argument ou en prendre plusieurs.

Un exemple de fonction sans argument :

def table7():
    """
    Show the 7 times table

    Args:
        None
    Returns:
        None
    """
    for i in range(11):
        print(f"{i} * 7 = {i*7}")

Avec deux ou trois arguments :

def pythagore(a, b):
    """
    Calculate the hypothenuse of the right triangle of legs a and b

    Args:
        a : positive float
        b : positive float
    Returns:
        the square of the length of the hypotenuse of the right triangle of legs a and b.
    """
    assert type(a) == float and type(b) == float," a and b must be float numbers."
    assert a >= 0 and b >= 0, "a and b must be positives."
    return a**2+b**2

def is_pythagore(a, b, c):
    """
    Determines if the triangle (a , b, c) is right at (a, b)

    Args:
        a : positive float
        b : positive float
    Returns:
        The square of the length of the hypotenuse of sides a and b
    """
    assert type(a) == float and type(b) == float," a and b must be float numbers."
    assert a >= 0 and b >= 0, "a and b must be positives."
    rep = False
    if c == pythagore(a, b): # Ici on fait appelle à la fonction définie avant
        rep = True
    return rep

Exercice : Ecrire une fonction somme_cube qui prend deux entiers p et q comme arguments et qui retourne \(\displaystyle\sum_{p}^q k^3\) .

Solution

def somme_cube(p:int, q:int)->int:
    """
    Calculate the sum of k^3 from p to q

    Args:
        p : a positive integer
        q : a positive integer p < q
    Returns:
        The sum of k^3 from p to q
    """
    assert type(p) == int and type(q) == int, "p and q must be integer."
    assert p >= 0, "p must be positive."
    assert q >= p, "q must be greater than p"
    s = 0
    for k in range(p,q+1):
        s += k**3
    return s

Exercice : Ecrire une fonction max2 qui prend deux nombres réels en argument et qui retourne le maximum des deux.

Solution

def max2(x:float, y:float)->float:
    """
    Determines which of x and y is greater.

    Args:
        x : a float number
        y : a float number
    Returns:
        max(x,y)
    """
    assert type(x) == float and type(y) == float, "x and y must be float numbers."

    if x <= y:
        rep = y
    else:
        rep = x
    return rep

Exercice : Ecrire une fonction max3 qui prend trois nombres réels en argument et qui retourne le maximum des trois.

Solution

def max3(x:float, y:float, z:float)->float:
    """
    Determines which of x, y and z is greater.

    Args:
        x : a float number
        y : a float number
        z : a float number
    Returns:
        max(x,y,z)
    """
    assert type(x) == float and type(y) == float and type(z) == float, "x, y and z must be float numbers."

    return max2(x,max2(y,z))

Exercice : Ecrire une fonction is_prime qui prend comme argument un entier n et qui retourne un booléen indiquant si n est premier ou non.

Solution

In [149]: def is_prime(n:int)->bool:
   .....:     """
   .....:     Test the primality of n
   .....:     Args:
   .....:         n : a positive integer
   .....:     Returns:
   .....:     True if n is prime, False otherwise.
   .....:     """
   .....:     assert type(n) == int, "n must be an integer."
   .....:     assert n >= 0, "n must be positive."
   .....:     rep = True
   .....:     if n in [0,1] or (n > 2 and n % 2 == 0):
   .....:         rep = False
   .....:     k = 3
   .....:     while rep and k**2 <= n:
   .....:         if n % k == 0:
   .....:             rep = False
   .....:         k += 2
   .....:     return rep
   .....: 

Exercice : Ecrire une fonction decompo_base qui prend deux entiers n et b et qui retourne sous forme de liste la décomposition de n dans la base b.

Note

Une fonction peut prendre comme argument… une autre fonction.

Par exemple :

In [150]: def cube(n:int)->int:
   .....:     """
   .....:     Calculate n**3
   .....:     Args:
   .....:         n : an integer
   .....:     Returns:
   .....:         n**3
   .....:     """
   .....:     assert type(n) == int, "n must be an integer."
   .....:     return n**3
   .....: 

Et

In [151]: from typing import Callable

In [152]: def somme_fk(f:Callable[[int],float], p:int, q:int)->float:
   .....:    """
   .....:    Calculate the sum of f(k) for k from p to q.
   .....:    Args:
   .....:        f : a function define on integer
   .....:        p : an integer
   .....:        q : an integer greater than p
   .....:    Returns:
   .....:        The sum of f(k) for k from p to q
   .....:    """
   .....:    assert type(p) == int and type(q) == int, "p and q must be integers numbers."
   .....:    assert p <= q, "q must be greater than p."
   .....:    somme = 0
   .....:    for i in range(p,q+1):
   .....:       somme += f(i)
   .....:    return somme
   .....: 

In [153]: print(somme_fk(cube, 0, 4))
100

Exercice : Ecrire une fonction produit_fk qui prend en argument une fonction \(f\) et deux entiers \(p<q\) et qui retourne le produit des nombres \(f(k)\) pour \(p\leq k\leq q\). Vérifiez votre résultat sur la fonction cube et la fonction factorielle .

Solution

from typing import Callable

def produit_fk(f:Callable[[int],float], p:int, q:int)->float:
    """
    Calculate the product of f(k) for k from p to q.

    Args:
        f : a real function define on integer
        p : an integer
        q : an integer greater than p
    Returns:
        the product of f(k) for k from p to q
    """
    assert type(p) == int and type(q) == int, "p and q must be integers numbers."
    assert p <= q, "q must be greater than p."

    p = 1
    for k in range(p, q+1):
        p *= f(k)
    return p

Les lambda

Note

Une fonction lambda est une fonction d’une seule ligne déclarée de manière anonyme (d’où le leur nom : lambda), qui peut avoir un nombre quelconque d’arguments, mais elle ne peut avoir qu’une seule expression. Il arrive souvent qu’une fonction lambda soit passée en argument à une autre fonction.

In [154]: f = lambda x, y : x + y

In [155]: f(2,3)
Out[155]: 5

In [156]: f("Hello ","World!")
Out[156]: 'Hello World!'

In [157]: somme_fk(lambda x : x**3, 0, 4)
Out[157]: 100

Types de données composées

Les listes

Note

Vous avez déjà vu comment créer une liste :

Par la description de ses éléments :

In [158]: liste1 = ['a',128,'Bob',3.14]

In [159]: liste1
Out[159]: ['a', 128, 'Bob', 3.14]

Par concaténation ou multiplication d’un ou plusieurs blocs :

In [160]: liste2 = liste1 + liste1

In [161]: liste2
Out[161]: ['a', 128, 'Bob', 3.14, 'a', 128, 'Bob', 3.14]

In [162]: liste3 = liste1 * 3

In [163]: liste3
Out[163]: ['a', 128, 'Bob', 3.14, 'a', 128, 'Bob', 3.14, 'a', 128, 'Bob', 3.14]

On peut aussi les définir en compréhension :

In [164]: liste4 = [i**2 for i in range(5)]

In [165]: liste4
Out[165]: [0, 1, 4, 9, 16]

In [166]: liste5 = [1 for i in range(5)]

In [167]: liste5
Out[167]: [1, 1, 1, 1, 1]

In [168]: liste6 = [2*i+1 for i in range(-3,6) if i % 4 != 0]

In [169]: liste6
Out[169]: [-5, -3, -1, 3, 5, 7, 11]

In [170]: liste7 = [k for k in range(30) if is_prime(k)]

In [171]: liste7
Out[171]: [2, 3, 5, 7, 11, 13, 17, 19, 23, 29]

Notez bien la puissance de cette manière de définir une liste.

Exercice : Créer une liste liste1 dont les éléments sont les cubes des entiers compris entre \(-10\) et \(20\) qui ne sont ni multiples de \(2\) ni de \(3\) .

Solution

In [172]: [k**3 for k in range(-10,21) if (k % 2 != 0 and k % 3 != 0)]
Out[172]: [-343, -125, -1, 1, 125, 343, 1331, 2197, 4913, 6859]

Exercice : En utilisant la fonction randint du module random, créer une liste de \(20\) nombres entiers aléatoires compris entre \(-100\) et \(100\).

Solution

In [173]: from random import randint

In [174]: [randint(-100,100) for _ in range(20)]
Out[174]: 
[-49,
 -47,
 41,
 12,
 -44,
 94,
 -34,
 75,
 -75,
 -41,
 66,
 -55,
 -47,
 57,
 9,
 -20,
 -67,
 51,
 -50,
 -58]

Note

Une liste est une collection ordonnées d’objets séparés par des virgules et encadrée par des crochets.

Par exemple :

In [175]: l1 = ['a',1]

In [176]: l2 = [1,'a']

In [177]: l1 == l2
Out[177]: False

Pour obtenir la longueur d’une liste on utilise la fonction len.

In [178]: l3 = [1,'a',3.14]

In [179]: len(l3)
Out[179]: 3

Pour accéder aux éléments d’une liste on utilise son indice (attention on commence à \(0\)) :

In [180]: l3[0]
Out[180]: 1

In [181]: l3[1]
Out[181]: 'a'

In [182]: l3[2]
Out[182]: 3.14

Les listes sont itérables, en particulier on peut les parcourir avec une boucle for:

In [183]: for i in range(len(l3)):
   .....:     print(l3[i])
   .....: 
1
a
3.14

On peut obtenir une tranche (un slice) d’une liste :

In [184]: l = list(range(21))

In [185]: l[2:7]
Out[185]: [2, 3, 4, 5, 6]

In [186]: l[::3]
Out[186]: [0, 3, 6, 9, 12, 15, 18]

In [187]: l[1:20:5]
Out[187]: [1, 6, 11, 16]

Les listes sont mutables (on peut les modifier) :

In [188]: l = [1,2]

In [189]: l[0] = 3

In [190]: l
Out[190]: [3, 2]

On peut tester l’appartenance d’un élément à une liste l grâce à l’expression x in l.

In [191]: l = [1,2,'coucou']

In [192]: 1 in l
Out[192]: True

In [193]: 'coucou' in l
Out[193]: True

In [194]: 3 in l
Out[194]: False

Exercice : Essayer les méthodes append, extend, count, insert, remove, reverse et sort, après avoir lu leur documentation grâce à help(list).

Exercice : Ecrire une procédure swap(l:list, i:int, j:int) , i.e. une fonction qui ne retourne rien, mais qui échange dans la liste l les éléménts en position i et j , après avoir vérifié que i et j sont des indices valables.

Solution

def swap(l:list, i:int, j:int):
    """
    Swap l[i] and l[j] if it's possible.

    Args:
        l : a real function define on integer
        i : an integer
        j : an integer
    Returns:
        Nothing
    """
    assert type(i) == int and type(j) == int, "i and j must be integers"
    assert 0 <= i < len(l) and 0 <= j < len(l),"i and j must be in range 0, len(l)-1

    l[i], l[j] = l[j], l[i]

Exercice : Ecrire une fonction is_in(elt:Any, l:list)->bool qui teste si elt est ou non dans la liste list. (Sans utiliser in).

Solution

from typing import Any

def is_in(elt:Any, l:list)->bool:
    """
    Test if elt is in l.

    Args:
        elt : an element
        l   : a list
    Returns:
        True if elt in l, False otherwise.
    """

    rep = False
    i = 0
    while i < len(l) and not rep:
        if l[i] == elt:
            rep = True
        i += 1
    return rep

Exercice : Ecrire une fonction positions(elt:Any, l:list)->list qui retourne la liste, éventuellement vide des indices des occurences de elt dans la liste l.

Solution

from typing import Any

def positions(elt:Any, l:list)->list:
    """
    Find positions of elt in l.

    Args:
        elt : an element
        l   : a list
    Returns:
        The list of indices of the positions of elt in the list l.
    """

    rep = []
    i = 0
    while i < len(l):
        if l[i] == elt:
            rep.append(i)
        i += 1
    return rep

Exercice : Ecrire une fonction maximum(l:list[float])->list qui retourne la liste formé du maximum de la liste de nombres list et de l’indice de la première position de ce maximum dans la liste.

Solution

def maximum(l:list[float])->(float, int):
    """
    Find the maximum of the list l and his first position.

    Args:
        l   : a list of float.
    Returns:
        the tuple (max, ind_max)
    """

    max_tmp = l[0]
    max_ind = 0
    i = 0
    while i < len(l):
        if l[i] > max_tmp:
            max_tmp = l[i]
            max_ind = i
        i += 1
    return (max_tmp, max_ind)

Exercice : Ecrire une fonction is_increasing(l:list[float])->bool qui teste si une fonction est croissante ou non et retourne le booléen correspondant.

Solution

def is_increasing(l:list[float])->bool:
    """
    Test if a list of float is increasing

    Args:
        l   : a list of float.
    Returns:
        True if l is increasing, False otherwise.
    """

    rep = True
    i = 0
    while rep and i < len(l)-1:
        if l[i+1] < l[i]:
            rep = False
    return rep

Exercice : Ecrire une fonction largest_growing_sub_list(l:list[int])->list[int] qui retourne la plus longue sous-liste croissante, constituée de termes consécutifs, d’une liste passée en argument.

Solution

def largest_growing_sub_list(l:list[int])->list[int]:
    """
    Find the largest increasing sublist in l.

    Args:
        l   : a list of int.
    Returns:
        The largest increasing sublist in l.
    """
    rep1 = [l[0]]
    rep2 = []
    for i in range(1,len(l)):
          if len(rep1) == 0 or rep1[-1] <= l[i]:
                rep1.append(l[i])
          elif len(rep2) < len(rep1):
              rep2 = rep1
              rep1 = []
          else:
              rep1 = []
    return rep1

Exercice : Ecrire une fonction qui teste si une liste liste1 se trouve dans une autre liste liste2 à la position n. On n’utilisera pas de slicing mais un test de correspondance élément par élément.

Solution

def is_sublist(l1:list[Any], l2:list[Any], n:int)->bool:
    """
    Test if l2 is a sub_list of l1 at position n.

    Args:
        l1 : a list.
        l2 : a list
        n  : an int
    Returns:
        True if l2 is a sublist of l1 at position n, False othewise.
    """
    if len(l2) + n > len(l1):
        rep = False
    else:
        rep = True
        i = n
        while rep and i < n + len(l2) - 1:
            if l1[i] == l2[i-n]:
                i += 1
            else:
               rep = False
    return rep

Exercice : Ecrire une fonction positions_dans_liste qui retourne la liste des positions d’une sous liste liste1 dans une liste liste2.

Solution

def positions_sublist(l1:list[Any], l2:list[Any])->list[int]:
    """
    Determine the list of positions of l2 as a sublist of l1.

    Args:
        l1 : a list.
        l2 : a list
    Returns:
        List of positions of l2 as sublist of l1.
    """
    rep = []
    for i in range(len(l1)-len(l2)):
        if is_sublist(l1,l2,i):
            rep.append(i)
    return rep

Exercice : Ecrire une fonction del_n_return(l:list[Any],i:int)->list[Any] qui retourne supprime l’élément d’indice i dans la liste et le retourne. On n’utilisera pas la méthode pop.

Solution

def del_n_return(l:list[Any], i:int)->list[Any]:
    """
    Removes the item at the given index from the list and returns the removed item.

    Args:
        l   : a list.
        i   : an int.
    Returns:
        l[i] after delete it in l.
    """

    rep = l[i]
    l = l[:i] + l[i+1:]
    return rep

Exercice : Ecrire une fonction nth_max(l:list[float], n:int)->float qui retourne le n-ième plus grand élément de l, après avoir testé que l contient assez d’éléments. Vous n’utiliserez pas les méthodes sort ou index, mais vous utiliserez les fonctions del_n_return et maximum que vous avez codé plus haut.

Solution

def nth_max(l:list[float], n:int)->float:
    """
    Determines the n-th largest number of l.

    Args:
        l   : a list of float.
    Returns:
        The n-th largest number of l.
    """

    assert n < len(l), "n is too large."
    lmax = []
    while len(lmax) < n:
        lmax.append(del_n_return(l,maximum(l)[1]))
    return lmax[len(lmax)-1]

Exercice : Ecrire une fonction filtre(l:list[int], test:Callable[[int], bool])->list[int] qui retourne la liste des éléments elt de la liste l pour lesquels test(elt) est True.

Solution

def filtre(l:list[int], test:Callable[[int], bool])->list[int]:
    """
    Selecte element of l which verify test(elt) == True

    Args:
        l      : a list of int
        test   : a function
    Returns:
        The list of elements of l for which test is true.
    """
    rep = []
    for elt in l:
        if test(elt):
            rep.append(elt)

    return rep

La bonne alternative en Python3

[elt in l if test(elt)]

Exercice : Ecrire une fonction chr_pos(l:list[str], c:str, n:int)->list[str] qui prend comme argument une liste l de mots, un caractère c et un entier n et qui retourne la liste des mots de l qui ont le cracatère c en position n.

Solution

def chr_pos(l:list[str], c:str, n:int)->list[str]:
    rep = []
    for mot in l:
        if len(mot) > n and mot[n] == c:
            rep.append(mot)
    return rep

Les tuples

Note

Un n-uplet ou tuple est une collection ordonnées d’objets séparés par des virgules et encadrée par des parenthèses.

Par exemple :

In [195]: t1 = ('a',1)

In [196]: t2 = (1,'a')

In [197]: t1 == t2
Out[197]: False

Pour obtenir la longueur d’un tuple on utilise la fonction len.

In [198]: t3 = (1,'a',3.14)

In [199]: len(t3)
Out[199]: 3

Pour accéder aux éléments d’un tuple on utilise son indice (attention on commence à \(0\)) comme pour le listes :

In [200]: t3[0]
Out[200]: 1

In [201]: t3[1]
Out[201]: 'a'

In [202]: t3[2]
Out[202]: 3.14

Les tuples sont itérables, en particulier on peut les parcourir avec une boucle for:

In [203]: for i in range(len(t3)):
   .....:     print(t3[i])
   .....: 
1
a
3.14

On peut obtenir une tranche (un slice) d’un tuple :

In [204]: t = tuple(range(21))

In [205]: t[2:7]
Out[205]: (2, 3, 4, 5, 6)

In [206]: t[::3]
Out[206]: (0, 3, 6, 9, 12, 15, 18)

In [207]: t[1:20:5]
Out[207]: (1, 6, 11, 16)

Contrairement aux listes, les tuples sont non-mutables :

In [208]: t = (1,2)

In [209]: t[0] = 3
---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
Input In [209], in <cell line: 1>()
----> 1 t[0] = 3

TypeError: 'tuple' object does not support item assignment

On peut tester l’appartenance d’un élément à un tuple t grâce à l’expression x in t.

In [210]: t = (1,2,'coucou')

In [211]: 1 in t
Out[211]: True

In [212]: 'coucou' in t
Out[212]: True

In [213]: 3 in t
Out[213]: False

Exercice : Ecrire une fonction copy_tuple(t:tuple)->tuple qui retourne un tuple copie du tuple t en utilisant une liste.

Solution

def copy_tuple(t:tuple)->tuple:
    """
    Return a copy of the tuple t.

    Args:
        t : the tuple to copy
    Returns:
        a copy of the tuple t
    """
    tmp_list = []
    for elt in t:
        tmp_list.append(elt)

    return tuple(tmp_list)

Exercice : Ecrire une fonction indice(elt:Any, t:tuple)->int qui retourne l’indice de la première occurence de elt dans t, si elle existe et -1 sinon.

Solution

def indice(elt:Any, t:tuple)->int:
    """
    Return the index of elt in tuple.

    Args:
        elt : an element
        t   : a tuple
    Returns:
        the index of elt in t if exists, or -1.
    """
    if not elt in t:
        rep = -1
    else:
        rep = 0
        while t[rep] != elt:
            rep += 1
    return rep

Exercice : Ecrire une fonction nb_occurences(elt:Any, t:tuple)->int qui retourne le nombre d’occurence de l’élément elt dans le tuple tuple.

Solution

def nb_occurences(elt:Any, t:tuple)->int:
    """
    Count the number of occurrences of elt in t.

    Args:
        elt : an element
        t   : a tuple
    Returns:
        The number of occurrences of elt in t.
    """
    rep = 0
    if elt in t:
        for e in t:
            if e == elt:
                rep += 1
    return rep

Exercice : Ecrire une fonction mdlast(l:list[tuple[int]],val:int)->list[tuple[int]] qui prend comme arguments une liste de tuples d’entiers et une valeur, et qui retourne la même liste de tuples après avoir remplacer le dernier élément de chaque tuple par la valeur.

Solution

def mdlast(l:list[tuple[int]], val:int)->list[tuple[int]]:
    """
    Change the last value of each tuple in list by val.

    Args:
        l    : a list of tuple of int
        val  : a int
    Returns:
        The same list where the last value of each tuple is val.
    """
    rep = []
    for t in l:
        l_tmp = list(t)
        l_tmp[-1] = val
        rep.append(tuple(l_tmp))
    return rep

Petit problème 2 :

Dans cet exercice, on cherche une approximation de \(\pi\) par une méthode de Monte-Carlo qui consiste à:

• tirer aléatoirement et uniformément un point M de coordonnées \((x,y)\) dans le carré unité \((x,y) \in [0,1[^2\)

• déterminer si le point se trouve dans le quart de cercle de rayon unité \(x^2 + y^2 \leq 1\)

• lancer cette expérience un grand nombre de fois et évaluer le ratio entre le nombre de points dans le quart de cercle et le nombre total de points. Ce ratio tend vers \(\displaystyle\frac{\pi}{4}\).

Pour cela, on utilisera la fonction random.random() qui permet de générer pseudo-aléatoirement un nombre entre 0 et 1. Elle est accessible après avoir fait import random.

Solution

In [214]: import random

In [215]: import math

In [216]: M = 10**3

In [217]: echantillons_dans_le_cercle = 0

In [218]: for (x,y) in ((random.random(), random.random()) for i in range(M)):
   .....:     if x**2+y**2 <= 1:
   .....:         echantillons_dans_le_cercle += 1
   .....: 

In [219]: print("Estimation de pi/4 ({}) : {}".format(math.pi/4.0,echantillons_dans_le_cercle/M))
Estimation de pi/4 (0.7853981633974483) : 0.762

Note

L’avantage d’un tuple sur une liste est qu’il est hashable .

Les dictionnaires

Note

Les dictionnaires sont des tableaux associatifs qui associent à chaque clef une valeur. Les clefs comme les valeurs peuvent être hétérogènes (i.e. de type différents). Seule restriction les clefs doivent être des objets hashables, donc non mutables, en particulier pas des listes ou des ensembles.

On définit des dictionnaires entre accolades et en déclarant les couples clef-valeur comme suit :

In [220]: dict1 = {'bananes': 4, 'citrons': 2.5, 'pamplemousses' : 'beaucoup', 3 : [1,2,3]}

On accède aux différentes valeurs à l’aide de leur clef :

In [221]: dict1['bananes']
Out[221]: 4

In [222]: dict1['citrons']
Out[222]: 2.5

In [223]: dict1['pamplemousses']
Out[223]: 'beaucoup'

In [224]: dict1[3]
Out[224]: [1, 2, 3]

Que se passe-til si l’on cherche à accéder à une valeur pour une clef qui n’existe pas :

In [225]: dict1['cerises']
---------------------------------------------------------------------------
KeyError                                  Traceback (most recent call last)
Input In [225], in <cell line: 1>()
----> 1 dict1['cerises']

KeyError: 'cerises'

On peut éviter cela en utilisant la méthode get :

# Comme second argument on donne une valeur qui sera retournée si la clef est absente.
In [226]: dict1.get('cerises', "Il n'y en a pas")
Out[226]: "Il n'y en a pas"

In [227]: dict1.get('cerises',0)
Out[227]: 0

On obtient la longueur d’un dictionnaire avec len:

In [228]: len(dict1)
Out[228]: 4

Il est possible d’accéder aux clefs et aux valeurs en utilisant les méthodes keys et values :

In [229]: dict1.keys()
Out[229]: dict_keys(['bananes', 'citrons', 'pamplemousses', 3])

In [230]: dict1.values()
Out[230]: dict_values([4, 2.5, 'beaucoup', [1, 2, 3]])

Il est possible d’itérer sur les clefs et/ou les valeurs :

In [231]: for key in dict1.keys(): print(dict1[key])
4
2.5
beaucoup
[1, 2, 3]

In [232]: for val in dict1.values(): print(val)
4
2.5
beaucoup
[1, 2, 3]

# Plus simplement
In [233]: for val in dict1: print(val)
bananes
citrons
pamplemousses
3

In [234]: for k, v in dict1.items(): print(k, v)
bananes 4
citrons 2.5
pamplemousses beaucoup
3 [1, 2, 3]

Les dictionnaires sont mutables :

# On peut modifier une valeur :
In [235]: dict1['bananes'] = 6

In [236]: dict1
Out[236]: {'bananes': 6, 'citrons': 2.5, 'pamplemousses': 'beaucoup', 3: [1, 2, 3]}

# On peut éliminer un coupl clef-valeur :
In [237]: dict1.pop('pamplemousses') # Comme pour la méthode de liste l'entrée est retournée.
Out[237]: 'beaucoup'

In [238]: dict1
Out[238]: {'bananes': 6, 'citrons': 2.5, 3: [1, 2, 3]}

# On peut ajouter un couple clef-valeur :
In [239]: dict1['pommes'] = 10

In [240]: dict1
Out[240]: {'bananes': 6, 'citrons': 2.5, 3: [1, 2, 3], 'pommes': 10}

Il est possible de définir un dictionnaire en compréhension comme pour les listes :

In [241]: dict2 = { x : x**3 for x in range(5)}

In [242]: dict2
Out[242]: {0: 0, 1: 1, 2: 8, 3: 27, 4: 64}

Comme pour les tuples et les listes on peut tester l’appartenance d’une clef avec in :

In [243]: 3 in dict2
Out[243]: True

Parmi les choses intéressantes avec les dictionnaires il y l’unpacking dont le principe est illustré ci-dessous :

In [244]: def prod(a,b):
   .....:     return a*b
   .....: 

In [245]: dict3 = {'a' : 2, 'b' : 3}

# On utilise ** pour "unpacker" le dictionnaire :
In [246]: prod(**dict3)
Out[246]: 6

Pour tout savoir sur les dictionnaires c’est ici .

Exercice : Ecrire une fonction find_key(d:dict, val:Any)->Any qui recherche la ou les clefs associées à la valeur val dans le dictionnaire d et en retourne la liste, et None si il n’y a aucune clef.

Solution

def find_key(d:dict, val:Any)->Any:
    """
    Find keys of value = val.

    Args:
        d   : a dict
        val : a value
    Returns:
        The list of keys of d of value = val.
    """

    rep = []
    for k, v in d.items():
        if v == val:
            rep.append(k)
    if len(rep) == 0:
        rep = None
    return rep

Exercice : Ecrire une fonction nb_occurences2(s:str)->dict qui prend une chaine de cractères en argument et qui retourne sous forme d’un dictionnaire le nombre d’occurence de chaque lettre qui apparait dans s.

Solution

def nb_occurences2(s:str)->dict:
    """
    Determine the number of occurencies of each character in string s.

    Args:
        s   : a string
    Returns:
        The dict of occurencies of each character in s.
    """

    occ = {}
    for c in s:
        occ[c] = occ.get(c,0) + 1
    return occ

Exercice : Pour la classe de PTSI-B on dispose d’un dictionnaire dont les clefs sont les noms des étudiants et les valeurs des listes de notes (pas nécessairement de même longueur). Ecrire une fonction average(d:dict)->dict qui retourne un dictionnaire dont les clefs sont les noms des étudiants et les valeurs leurs moyennes.

Solution

def average(d:dict)->dict:
    """
    Calculate averages of students.

    Args:
        d   : a dict
    Returns:
        The dict of averages.
    """

    ave = {}
    for student in d:
        notes = d[student]
        if len(notes) > 0:
            s = 0
            for note in notes:
                s += note
            m = s/len(notes)
            ave[student] = m
        else:
            ave[student] = 'Non noté'

    return ave

Exercice : Ecrire une fonction matching_score(d1:dict, d2:dict)->int qui prend comme argument deux dictionnaires d1 et d2 et qui comptabilise le score de correspondances entre le premier et le second de la manière suivante : pour chaque clef key de d1, si key est une clef de d2 on ajoute 3 au score si les valeurs correspondantes sont les mêmes, -2 si elle diffèrent, enfin si la clefs n’est pas présente dans d2 on ajoute -1.

Solution

def matching_score(d1:dict, d2:dict)->int:
    """
    Calculate the matching's score of d1 and d2.

    Args:
        d1 : a dict
        d2 : a dict to score the matching with d1
    Returns:
        The matching's score of d2.
    """

    score = 0
    for k, v in d1.items():
        if not k in d2:
            score += -3
        elif v == d2[k]:
            score += 3
        else:
            score += -3

    return score

Exercice : Ecrire une fonction creat_dict_pos(l:list[str])->list[str], qui prend comme argument une liste de mots et qui retourne le dictionnaire dont les clefs sont les tuples ('c',n) et les valeurs la liste des mots de l qui comporte le caractère c en position n. Quel est l’intérêt de cette fonction par rapport à chr_pos (codée plus haut) ?

Solution

def create_dic(mots):
    pos = {}
    for mot in mots:
    for i in range(len(mot)):
        if (mot[i], i) in pos:
            pos[(mot[i],i)].append(mot)
        else:
             pos[(mot[i], i)] = [mot]
    return pos