TP4 : Récursivité#

Note

Les objectifs du TP :

Écrire des algorithmes récursifs
Mettre en oeuvre la mémoïsation

Note

Si l’on souhaite écrire une fonction qui calcule $n!$ , au lieu de calculer tous les produits on peut écrire, pour $n>1$, que $n!=n\times (n-1)!$ et $1!=1$. Autrement dit, si $f$ est cette fonction alors elle vérifie :

$f(n)=n\times f(n-1)$ si $n>1$ et $f(1)=1$ .

On pourrait donc l’écrire :

def factorielle(n):
    if n == 1:
        return 1
    else:
        return n*factorielle(n-1)

Calculer de cette manière s’appelle la récursivité, la fonction s’appelle elle-même.

Une fonction récursive commence toujours par traiter ce qu’on appelle les conditions d’ârret, dans notre exemple il n’y en a qu’une, mais il peut y en avoir plusieurs.

En utilisant le décorateur suivant, vous pourrez observer les appels successifs d’une fonction récursive :

def trace(func):
    def wrapper(*args):
        print(' ' * wrapper.space, end='')
        print('{} <− {}'.format(func.__name__, str(args)))
        wrapper.space += 1
        val = func(*args)
        wrapper.space -= 1
        print(' ' * wrapper.space, end='')
        print('{} −> {}'.format(func.__name__, str(val)))
        return val
    wrapper.space = 0
    return wrapper

Prenons un exemple. Considérons la fonction suivante :

@trace
def s(a:int, b:int):
    if a == 0:
        return b
    else:
        return s(a-1,b+1)

Que calcule cette fonction ? Avec le décorateur on obtient :

>>> s(4,3)
s <− (4, 3)
 s <− (3, 4)
  s <− (2, 5)
   s <− (1, 6)
    s <− (0, 7)
    s −> 7
   s −> 7
  s −> 7
 s −> 7
s −> 7

Vous pouvez voir que la fonction a été appelée cinq fois, avant de retourner cinq fois… On dit qu’on a empilé les appels. Le nombres d’appels peut-être très important, ce qui est un problème. C’est ce qui nous intéressera à la fin du TP.

Ceux qu’il faut avoir programmés une fois#

Exercice :

Écrire une fonction exp1(a,n) qui prend comme arguments un nombre flottant a et un entier n et qui retourne $a^n$, en utilisant l’opérateur puissance de Python.

Écrire une deuxième fonction récursive exp2(a,n), qui retourne encore $a^n$, et qui exploite la relation $a^n = a\times a^{n-1}$.

Écrire une troisième fonction exp3(a,n), qui retourne toujours $a^n$, en exploitant la relation :

\[a^n = a^{\lfloor n/2\rfloor}\times a^{n-\lfloor n/2\rfloor}\]

Écrire une quatrième fonction exp4(a,n),qui retourne toujours $a^n$ , en exploitant la même relation, mais en exploitant en plus que :

\[\begin{split}n-\lfloor n/2\rfloor = \left\{\begin{array}{lr} \lfloor n/2\rfloor&\text{ si $n$ est pair.}\\ \lfloor n/2\rfloor + 1&\text{ sinon.}\end{array}\right.\end{split}\]

Modifier vos codes pour compter le nombre d’appels récursifs des fonctions.

Utiliser la fonction perf_counter() du module time pour mesurer le temps d’exécution de ces quatre fonctions par calculer $2^{900}$. Qu’observez-vous ?

Comparer le nombre d’appels récursifs des trois fonctions exp2(a,n), exp3(a,n) et exp4(a,n), pour $a=2$ et $n=100,\,200,\,400,\,800$.

Évaluez le nombre de multiplication effectuées par exp3(a,n) et exp4(a,n).

Solution

def exp1(a,n):
      return a**n


def exp2(a,n):
      if n == 0:
            rep = 1
      else:
            rep = a*exp2(a,n-1)
      return rep

def exp3(a,n):
      if n == 0:
            rep = 1
      elif n == 1:
            rep = a
      else:
            p = n // 2
            rep = exp3(a,p)*exp3(a,n-p)
      return rep


def exp4(a,n):
      if n == 0:
            rep = 1
      elif n == 1:
            rep = a
      elif n % 2 == 0:
            rep = exp4(a*a, n//2)
      else:
            rep = a*exp4(a*a, n//2)
      return rep

Exercice : Écrire une fonction récursive sum_digits(n) qui prend comme argument un entier $n$ et qui retourne la somme de ses chiffres.

Solution

def sum_digits(n):
    if n < 10:
        rep = n
    else:
        rep = (n%10)+ sum_digits(n//10)
    return rep

Exercice : Soient $a$ et $b$ deux flottants, on définit les suites $(u_n)$ par $u_0= a$ et $v_0=b$ et pour $n\geq 0$ :

\[u_{n+1} = \sqrt{u_n v_n} \text{ et }v_{n+1}=\dfrac{1}{2}\left(u_n+v_n\right).\]

Écrire deux fonctions récursives seq_u(n,a,b) et seq_v(n,a,b) qui retourne respectivement les valeurs de $u_n$ et $v_n$.

Exercice : Pour dénombrer $\mathbb{N}\times\mathbb{N}$, on peut utiliser la fonction de Cantor pour numéroter les éléments de $\mathbb{N}\times\mathbb{N}$ de la manière illustrée sur la figure suivante :

Écrire une fonction récursive pairing_function(x,y) qui prend comme argument un élément $(x,y)\in \mathbb{N}\times\mathbb{N}$ et qui retourne son numéro.

Solution

def pairing_function(x,y):
    if x == 0 and y == 0:
        return 0
    if y > 0:
        return 1 + pairing_function(x+1, y-1)
    return 1 + pairing_function(0, x-1)

Écrire, de manière récursive, la fonction réciproque inv_pairing_function(n) qui prend comme argument un entier $n$ et qui retourne le couple $(x,y)$ dont il est le numéro.

Solution

def inv_pairing_function(n):
    if n == 0:
        return (0,0)
    (x,y) = inv_pairing_function(n-1)
    if x > 0:
        return (x-1,y+1)
    return (y+1,0)

Exercice *Difficile* : Dans cet exercice on représente les ensembles d’entiers par des listes d’entiers deux à deux distincts. Écrire une fonction récursive list_of_subset(E) qui prend comme argument un ensemble et qui retourne l’ensemble de ses sous-ensembles. On pourra remarquer que si $E$ est un ensemble et si $a\in E$, alors les sous-ensembles de $E$ sont ceux de $E\setminus\{a\}$, et ceux de $E\setminus\{a\}$ auxquels on ajoute $a$.

Solution

def subset(E):
    if E == []:
        rep = [[]]
    else:
        E1 = subset(E[1:])
        E2 = [[E[0]] + s for s in E1]
        rep = E1 + E2
    return rep

De beaux dessins#

Note

Voici le code d’une fonction qui permet de tracer un cercle de centre $(x,y)$ et de rayon $r>0$ :

import matplotlib.pyplot as plt
fig, ax = plt.subplots()
ax.set_aspect(1)
plt.axis("equal")

def circle(x,y,r):
    ax.add_artist(plt.Circle((x,y),r,color ='r', fill = False))

Et voici celui d’une fonction qui trace un triangle plein dont les sommets sont $(x_1,y_1)$, $(x_2,y_2)$ et $(x_3,y_3)$ :

from matplotlib.patches import Polygon

def triangle(x1,y1,x2,y2,x3,y3):
    liste = [[x1,y1],[x2,y2],[x3,y3]]
    ax.add_patch(Polygon(liste, closed=True,fill=True, color='red'))

Pour régler le cadre d’affichage vous pouvez utiliser :

ax.set_xlim(x_min, x_max)
ax.set_ylim(y_min, y_max)

Exercice : Écrire une fonction récursive bubble1(n) qui prend comme argument un entier $n$, et qui permet d’obtenir la figure suivante pour $n=5$ :

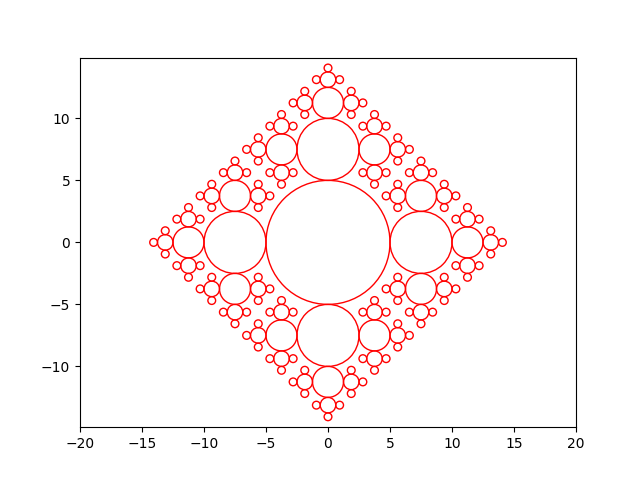
Exercice : Écrire une fonction récursive bubble2(n) qui prend comme argument un entier $n$, et qui permet d’obtenir la figure suivante pour $n=5$ :

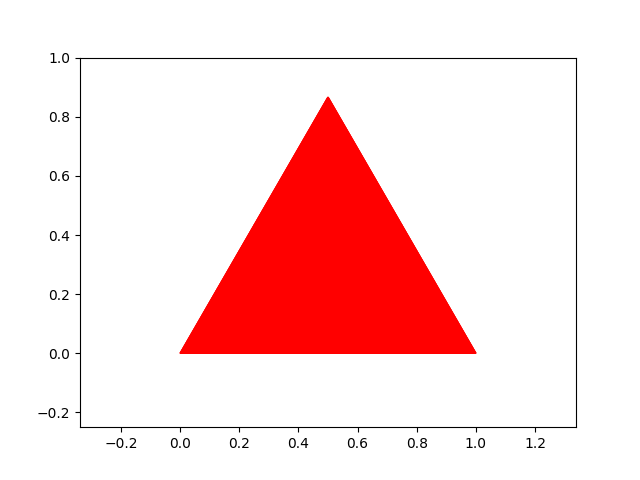
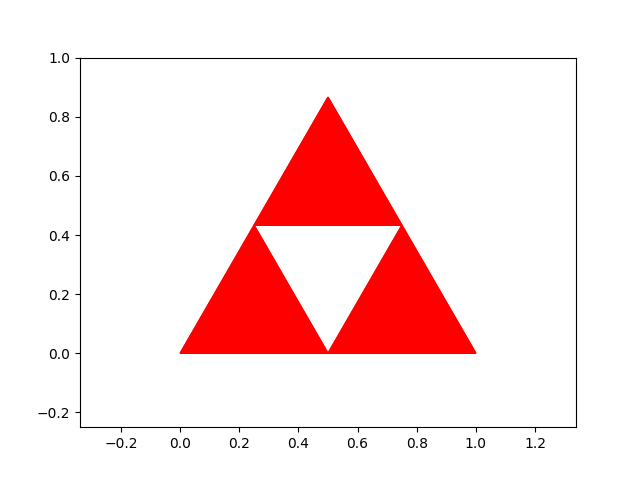
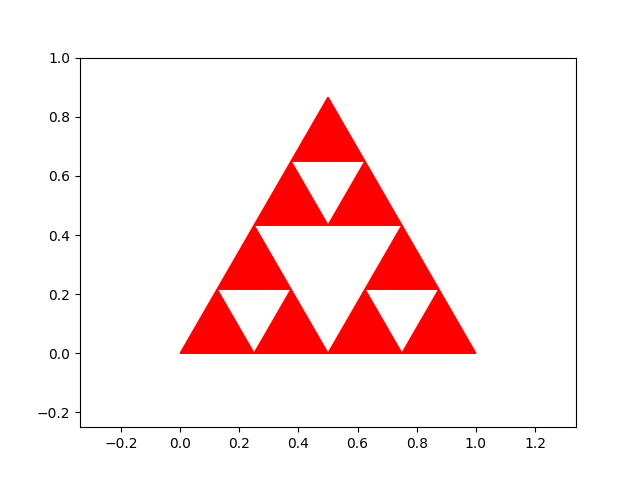
Exercice : Écrire une fonction récursive sierpinski(n) qui prend comme argument un entier $n$, et qui permet d’obtenir les figures suivantes pour $n=1,2,3$ et $4$ :

Tous les triangles sont équilatéraux.

Optimisations#

Mémoïsation#

Note

Nous pouvons diminuer les coûts temporels et spatiaux d’une fonction aux appels récursifs multiples en enregistrant les calculs déjà effectués dans une mémoire cache. Nous allons appliquer ce principe au calcul récursif du $n$-ième terme de la suite de Fibonacci.

Exercice : Écrire une fonction itérative fibo_it(n) qui prend comme argument un entier $n$ et qui retourne le $n$-ième terme de la suite de Fibonacci.

Exercice : Écrire une fonction récursive fibo_rec(n) qui prend comme argument un entier $n$ et qui retourne le $n$-ième terme de la suite de Fibonacci.

Exercice : Écrire une fonction récursive fibo_m(n) qui tire profit de la mémoïsation. Pour cela vous allez utiliser une liste comme cache pour stocker les résultats des calculs intermédiaires. Au départ vous initialiserez le cache avec les deux premiers termes de la suite : cache = {0 : 0, 1 : 1]. Ensuite avant de faire un appel récursif vous vérifierez si le terme que vous souhaitez calculer n’est pas déjà en cache.

Solution

cache = {0:0, 1:1}
def fibo_m(n):
    if n in cache:
        res = cache[n]
    else:
        cache[n] = fibo_m(n-1)+cache[n-2]
        res =  cache[n]
    return res

Question 4 : Écrire une fonction récursive avec mémoïsation fact_m(n) qui prend comme argument un entier $n$ et qui retourne $n!$.

Récursivité terminale et Tail Call Elimination#

Note

La Tail Call Elimination (TCE), également connue sous le nom d’optimisation de la récursivité terminale, est une technique d’optimisation couramment utilisée pour les langages de programmation fonctionnels tels que Scheme, mais elle peut également être appliquée à Python.

La TCE consiste à remplacer une récursivité terminale par une boucle, de sorte que la pile d’appels ne soit plus nécessaire pour exécuter la fonction, ce qui peut améliorer les performances et éviter un éventuel débordement de la pile d’appels.

Pour le faire il suffit de remarquer qu’un appel récursif terminal revient à effectuer un GOTO avec une mise à jour des différents paramètres. Prenons l’exemple de l’algorithme d’Euclide du calcul du pgcd : (on suppose $a>b$):

def pgcd_rec(a : int, b : int)->int:
    if b == 0:
        pgcd = a
    else:
        pgcd = pgcd_rec(b, a % b)
    return pgcd

L’appel récursif est bien terminal. Si l’on se sert de la condition d’arrêt comme condition d’une boucle while et que l’on mets les différentes variables à jour on obtient l’algoritme itératif suivant :

def pgcd(a : int,b : int)->int:
    while b > 0:
        a, b = b, a % b
    return b

Exercice : Effectuer une TCE sur la fonction suivante :

def s(a : int, b : int)->int
    if a == 0:
        return b
    else:
        return s(a-1,b+1)

Solution

def s(aint, bint)->int

while a > 0:
a -= 1 b += 1

return b

Exercice : Effectuer une TCE sur la fonction suivante :

def palindrome(mot : str)->bool:
    if len(mot) < 2:
        return True
    elif mot[0] != mot[-1]:
        return False
    else:
        return palindrome(mot[1:-1])

Solution

def palindrome(mot : str)->bool:
    rep = True
    while len(mot) > 1 and rep:
        print(mot)
        if mot[0] != mot[-1]:
            rep = False
        mot = mot[1:-1]
    return rep

Note

La TCE n’est possible que si la récursion est terminale. Dans certains cas il est possible de transformer une récursion quelconque en une récursion terminale. Pour cela on a recourt à des accumulateurs pour stocker les résultats intermédiaires et les passer comme argument lors de chaque appel récursif. Par exemple la fonction récursive suivante n’est pas terminale :

def somme(n : int)->int:
    if n == 0:
        return 0
    else:
        return n + somme(n-1)

Pour transformer cette fonction en une fonction récursive terminale, on peut utiliser un accumulateur pour stocker la somme partielle et le passer comme argument lors de chaque appel récursif :

def somme(n : int, acc = 0)->int:
    if n == 0:
        return acc
    else:
        return somme(n-1, acc+n)

Dans cette fonction, acc est l’accumulateur qui stocke la somme partielle. L’appel initial de la fonction utilise une valeur par défaut de 0 pour l’accumulateur. Lors de chaque appel récursif, la fonction passe acc+n comme nouvel accumulateur.

Exercice : Utiliser un accumulateur pour transformer la fonction récursive suivante :

def puissance(base : int, exposant : int):
    if exposant == 0:
        return 1
    else:
        return base * puissance(base, exposant - 1)

Solution

def puissance(base, exposant, accumulateur=1):
    if exposant == 0:
        return accumulateur
    else:
        return puissance(base, exposant - 1, accumulateur * base)

Exercice : Utiliser un accumulateur pour transformer la fonction récursive suivante :

def somme_carres(n : int)->int:
    if n == 0:
        return 0
    else:
        return n**2 + somme_carres(n-1)

Solution

def somme_carres(n : int, acc=0)->int:
    if n == 0:
        return acc
    else:
        return somme_carres(n-1, acc+n*n)

Exercice : Utiliser deux accumulateurs pour transformer la fonction récursive suivante :

def fibonacci(n : int)->int:
    if n in [0,1]:
        return n
    else:
        return fibonacci(n-1) + fibonacci(n-2)

Solution

def fibonacci(n, next=0, acc=1):
    if n == 0:
        return a
    elif n == 1:
        return b
    else:
        return fibonacci(n-1, next , acc + next)

Exercice : Utiliser un accumulateur (attention ce n’est pas un nombre) pour transformer la fonction récursive suivante :

def concat_strings(lst : list[str])->str:
    if len(lst)==0:
        return ''
    else:
        return lst[0] + concat_strings(lst[1:])

Solution

def concat_strings(lst, acc=""):
    if not lst:
        return acc
    else:
        return concat_strings(lst[1:], acc + lst[0])

Exercice :* Ecrire des versions itératives de toutes les dernières fonctions.

Les TP d informatique en PTSI-B

TP4 : Récursivité

Contents

TP4 : Récursivité#

Ceux qu’il faut avoir programmés une fois#

De beaux dessins#

Optimisations#

Mémoïsation#

Récursivité terminale et Tail Call Elimination#