TP8 : Applications des parcours de graphe

Note

Les objectifs du TP :

• Utiliser les parcours de graphe.

• Constuire la forêt couvrante d’un parcours.

• Appliquer les parcours à un problème concret.

• Implémenter ces algorithmes en Python.

Forêt couvrante

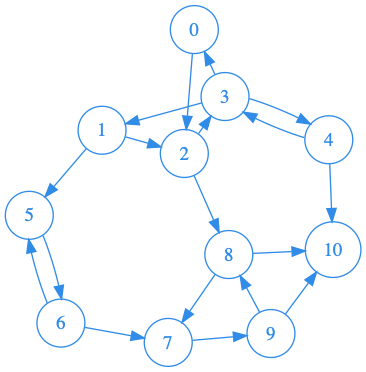
Fig. 1 Graphe 1

Code du graphe 1

G1 = {
    0 : [2],
    1 : [2, 5],
    2 : [3, 8],
    3 : [0, 1, 4],
    4 : [3, 10],
    5 : [6],
    6 : [5, 7],
    7 : [9],
    8 : [7, 10],
    9 : [8, 10],
    10 : []
    }

Exercice : Faire à la main le parcours profondeur du graphe de la figure 1, dessiner la forêt couvrante du parcours en notant les différents types d’arcs :

• arc couvrant

• arc retour

• arc croisé

• arc avant

Noter l’ordre préfixe et l’ordre suffixe de chaque sommet dans des tableaux.

Exercice : Ecrire une fonction de signature orders(G: dict)->tuple[list[int],list[int]] qui prend un graphe comme argument et retourne les deux listes pref et suff contenant à l’indice \(i\) l’ordre préfixe, respectivement suffixe, du sommet \(i\).

>>> orders(G1)
([1, 4, 2, 3, 11, 5, 6, 7, 9, 8, 10], [11, 7, 10, 9, 8, 6, 5, 4, 2, 3, 1])

Pour chaque arc \((x,y)\) du parcours comparer les ordres préfixes et suffixes de \(x\) et \(y\).

Solution

\[\begin{split}\begin{array}{|l|c|c|} \hline \textrm{avant} & pref(x)<pref(y) & suff(x)>suff(y) \\ \hline \text{couvrant} & pref(x)<pref(y) & suff(x)>suff(y) \\ \hline \text{croisé} & pref(x)>pref(y) & suff(x)>suff(y)\\ \hline \text{retour} & pref(x)>pref(y) & suff(x)<suff(y) \\ \hline \end{array}\end{split}\]

Exercice : Ecrire une procédure dfs_digraph_forest(G: dict)->None qui effectue le parcours profondeur du graphe orienté \(G\) et affiche lors de celui-ci les arcs de parcours et leur nature. Par exemple :

>>> dfs_forest(G1)
0 -> 2 arc couvrant
2 -> 3 arc couvrant
3 -> 0 arc retour
3 -> 1 arc couvrant
1 -> 2 arc retour
1 -> 5 arc couvrant
5 -> 6 arc couvrant
6 -> 5 arc retour
6 -> 7 arc couvrant
7 -> 9 arc couvrant
9 -> 8 arc couvrant
8 -> 7 arc retour
8 -> 10 arc couvrant
9 -> 10 arc en avant
3 -> 4 arc couvrant
4 -> 3 arc retour
4 -> 10 arc croisé
2 -> 8 arc en avant

Exercice : Ecrire une fonction dfs_graph_forest(G: dict)->None qui effectue le parcours profondeur du graphe non orienté \(G\) et affiche lors de celui-ci les arcs de parcours et leur nature.

Détection de cycle

Note

On rappelle la propriété suivante : Un graphe \(G\) est sans circuit si et seulement son parcours profondeur ne génère pas d’arc retour.

Exercice : Ecrire une fonction de signature is_acyclic(G: dict)->bool qui teste si un graphe orienté est acyclique.

Exercice : Ecrire une fonction de signature is_tree(G: dict)->bool qui teste si un graphe non orienté est un arbre.

Ordre topologique

Note

Etant donné un graphe orienté \(G=(S,A)\) d’ordre \(n\), on appelle ordre topologique sur \(G\) une numérotation \(num\,:\,S\to \{0,\ldots,n-1\}\) telle que :

\[\forall (x,y)\in A,\; num(x) <num(y).\]

En d’autres termes, si l’on parcourt la liste des sommets dans l’ordre defini par une telle numerotation, un sommet y ne peut être rencontre que si l’on a, au prealable, rencontre tous ses predecesseurs.

Fig. 2 Graphe 2

Code du graphe 2

G4 = {
    0 : [1, 4, 7],
    1 : [2, 7],
    2 : [5],
    3 : [2, 4],
    4 : [5],
    5 : [6],
    6 : [],
    7 : [6],
    8 : [7],
    }

Exercice :

• Quelle condition un graphe orienté doit-il remplir pour qu’un tri topologique existe ?

• Faire le parcours profondeur du graphe de la figure 2 et noter les ordres suffixes des sommets. Si \((x,y)\in A\), dans quel ordre sont rangés \(suff(x)\) et \(suff(y)\) ?

• Démontrer que l’ordre suffixe inversé est un tri topologique de \(G\).

• Déssiner le graphe \(G\) en alignant ses sommets dans l’ordre d’un tri topologique. Que remarquez-vous ?

• Lors d’un parcours profondeur, quelle structrure de données peut-on utiliser pour stocker les sommets en ordre suffixe, pour obtenir un tri topologique ?

• Ecrire une fonction tri_topo(G: dict)->list[int] qui prend comme argument un graphe, pour lequel il existe un tri topologique et qui le retourne.

Exercice : On souhaite construire une maison, le tableau suivant présente les différentes tâches à réaliser ainsi que leurs durées et les différentes contraintes qu’elles imposent.

Tâches		Durées	Contraintes
A	Achat terrain	2
B	Permis	3	A
C	Fondations	4	A, B
D	Préfabriqué	4
E	Assemblage	2	A, B, C
F	Couverture	3	D
G	Peinture	2	I, J, E, F
H	Menuiserie	4	E, F, I
I	Sanitaires	2	E
J	Eléctricité	2	E, F
K	Emménagement	1	A, B, C, D, E, F, G, H, I, J, K

• Trouver un ordre dans lequel effectuer toutes les tâches.

• Quelle est la durée minimum du chantier ?