TP9 : Plus courts chemins

Note

Les objectifs du TP :

• Implémenter Dijkstra avec un ensemble et une file de priorité.

• Utiliser Dikstra.

• Découvrir A*.

Note

Pour représenter une graphe pondéré on utilisera une structure de dictionnaire de dictionnaires.

Par exemple :

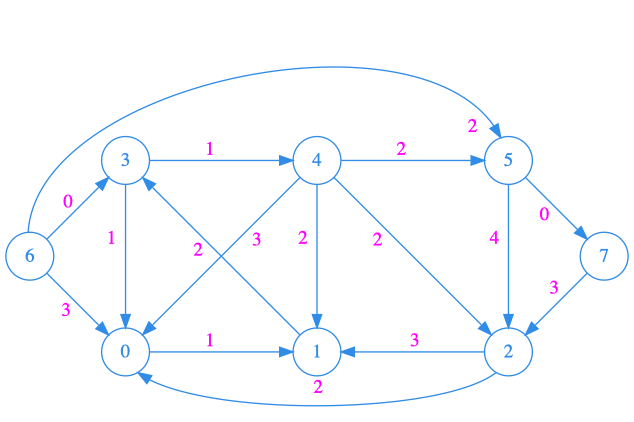
G = {
    0: {1: 1},
    1: {3: 2},
    2: {1: 3},
    3: {0: 1, 4: 1},
    4: {0: 3, 1: 2, 2: 2, 5: 2},
    5: {2: 4, 7: 0},
    6: {0: 3, 3: 0, 5: 2},
    7: {2: 3}
    }

représente le graphe :

De sorte que G[3] est un dictionnaire dont les clefs sont les successeurs du sommet 3, et tel que G[3][4] est le poids de l’arrête \((3, 4)\).

Variations autour de Dijkstra

Note

Pour rappel :

Exercice : Ecrire une fonction de signature dijkstra_set(G: dict, src: int)->tuple[list[int],list[int]], qui prend comme argument un graphe G pondéré sous forme de dictionnaire de dictionnaires, et un sommet src, et qui retourne les listes dict et pred, respectivement des distances à src et des prédecesseurs dans le plus court chemin de src à un sommet s . L’algorithme utilisera une ensemble comme décrit dans le cours.

Solution

inf = float('inf')

def min_dist(dist,M):
    s = None
    mini = inf
    for i in range(len(dist)):
        if i in M and dist[i] < mini:
            s = i
            mini = dist[i]
    return s

def dijkstra_set(G: dict, src: int)->tuple[list[int],list[int]]:

    n = len(G)

    dist = [inf] * n
    pred = [None] * n

    pred[src] = -1
    dist[src] = 0

    M = set(range(n))

    s = src

    while s != None and len(M) > 0:
        M.discard(s)
        for v in G[s]:
            if dist[s] + G[s][v] < dist[v]:
                dist[v] = dist[s] + G[s][v]
                pred[v] = s
        s = min_dist(dist, M)

    return dist, pred

Exercice : Ecrire une seconde fonction de signature dijkstra_heap(G: dict, src: int)->tuple[dict,dict], qui prend comme argument un graphe G sous forme de dictionnaire de dictionnaires, et un sommet src, et qui retourne les dictionnaires dist et pred, respectivement des distances à src et des prédecesseurs dans le plus court chemin de src à un sommet s. L’algorithme utilisera un file de priorité comme décrit dans le cours. Vous utiliserez le module heap fourni avec le TP.

Solution

from heap import *

def dijkstra_heap(G: dict, src: int):

    n = len(G)
    dist, pred = {}, {}
    for node in G.keys():
        dist[node] = inf
        pred[node] = None

    pred[src] = -1
    dist[src] = 0

    M = Heap([])

    M.push((dist[src],src))

    while len(M)>0:

        _, s = M.pop()

        for v in G[s]:
            d = dist[v]
            if dist[s] + G[s][v] < dist[v]:
                dist[v] = dist[s] + G[s][v]
                pred[v] = s
                M.update((d, v), (dist[v], v))


    return pred, dist

Exercice : Utiliser la fonction alea_directed_graph, qui se trouve dans le module TP9 pour générer des graphes orientés et pondérés de tailles \(100*2^k\) pour \(1\leq k\leq 7\), et comparer les temps d’exécution des deux fontions dijkstra_set et dijkstra_heap. Que constatez-vous ?

Exercice : Ecrire une fonction de signature build_path(pred: dict, src, dst):->list qui retourne la liste des sommets qui constituent le plus court chemin de src à dst.

Solution

def build_path(pred: dict, src , dst):
    path = []
    node = dst

    while pred[node] != -1:
        path = [node] + path
        node = pred[node]
    path = [src] + path
    return path

Exercice : Modifier le code la fonction dijkstra_heap, pour écrire une nouvelle fonction de signature dijkstra(G: dict, src: int, dst: int)->float, list[int], qui retourne le plus court chemin de src à dst dans le graphe G, s’il existe, ainsi que sa longueur, et None sinon. Vous veillerez à arrêter l’agorithme dès que la destination dst est atteinte.

Exercice (bonus) : Ecrice une fonction round_trip(G: dict, src: int, dst: int)->list[int] qui retourne, s’il existe, le plus court chemin aller-retour de src à dst qui au retour ne passe pas par les mêmes sommets qu’à l’aller.

L’algorithme A*

Note

L’algorithme A* est un algorithme de recherche de chemin dans un graphe entre un noeud initial src et un noeud final dst. Il utilise une évaluation heuristique sur chaque noeud pour estimer le meilleur chemin y passant, et visite ensuite les noeuds par ordre de cette évaluation heuristique. Vous trouverez de nombreuses informations ici.

Imaginons que le graphe que l’on va parcourir représente les cases d’un plateau sur lequel on souhaite se déplacer.

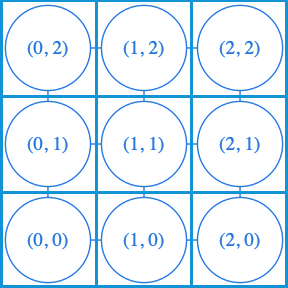
Si nous souhaitons trouver le chemin le plus court du sommet (0, 0) au sommet (2, 2). L’application de l’algorithme de Dijkstra, va visiter les neuf points du sommets du graphe, en procédant à un parcours largeur. Notre intuition est que des trois sommets (1, 0), (1, 1) et (0, 1), nous devrions dès le début privilégier celui qui nous rapproche le plus de la destination, soit le (1, 1).

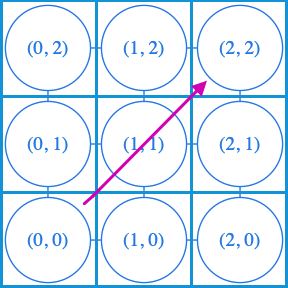
Pour déterminer quelle est la bonne direction on peut utiliser comme heuristique h la distance entre le noeud étudié et la déstination, quelque soit cette distance (distance euclidienne, distance de Manhattan, etc…). Dans ce cas, la priorité avec laquelle on doit traiter un sommet est donnée par la minimisation de la quantité dist[s]+h(s,dst), où dist[s] est la distance de src à s, et h(s, dst) est la distance de s à la destination dst.

Si l’heuristique est la fonction identiquement nulle, on retombe sur Dijkstra.

Exercice : Implémenter une fonction de signature A_star(G: dict, h: callable, src: tuple[int,int], dst:tuple[int,int])->list[int],int, int, qui prend comme argument un graphe, une heuristique, un sommet source et un sommet destination et qui retourne le dictionnaire pred des prédecesseurs dans le plus court chemin trouvé entre src et dst, s’il existe. Ainsi que le nombre de sommets visités lors de la recherche du chemin, et le nombre d’itération de la boucle principale effectuées pour déterminer le chemin.

Solution

Note

Dans le module TP9, vous trouverez les graphes qui représentent les plateaux suivants :

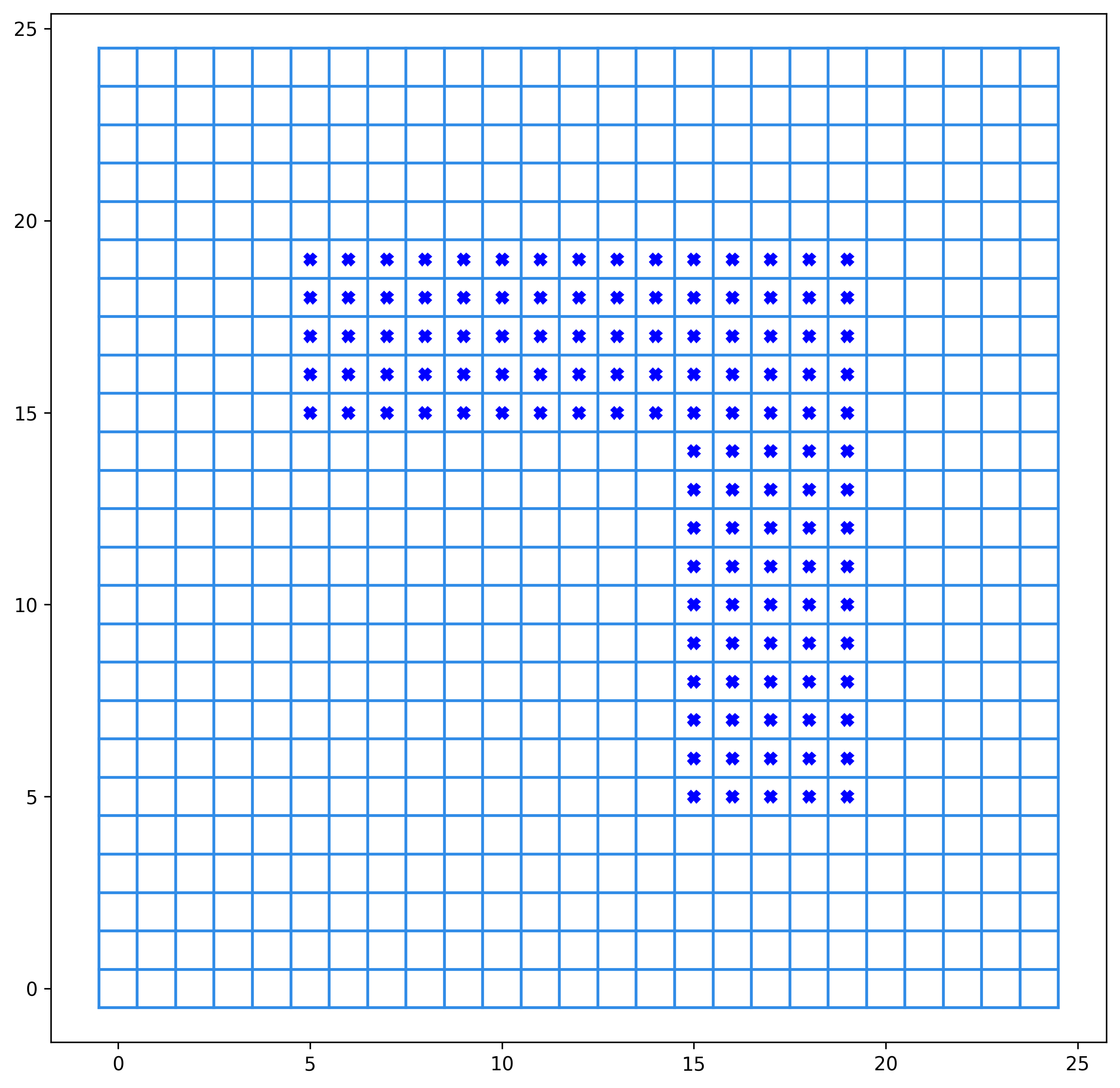
Fig. 3 Graphe G1

Fig. 4 Graphe G2

Fig. 5 Graphe G3

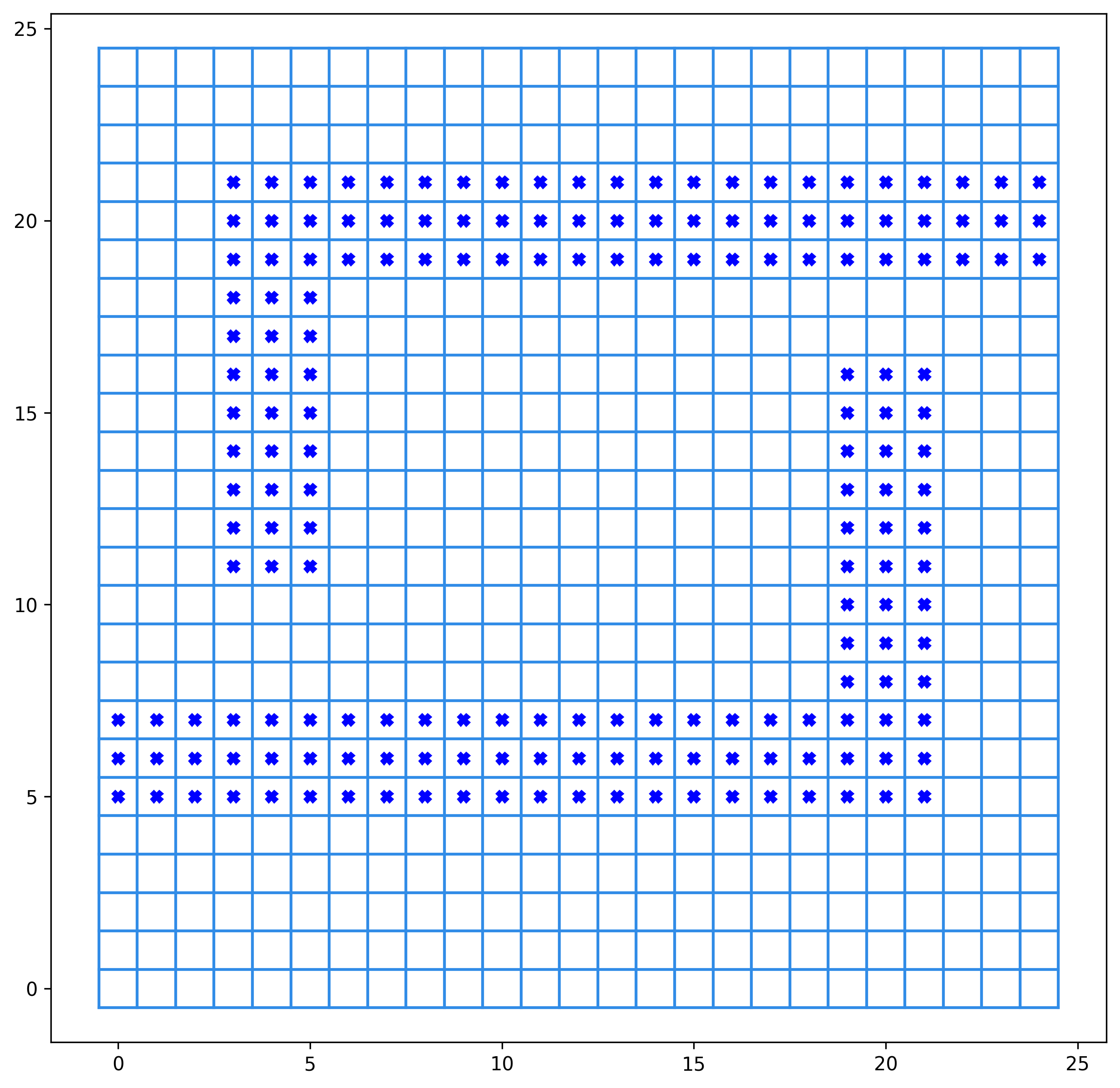
Fig. 6 Graphe G4

Fig. 7 Graphe G5

Le but de cette partie et de voir quelles solutions sont proposées par Dijkstra et par A* pour aller de la case en bas à gauche à la case en haut à droite.

Vous avez à votre disposition les fonctions du module TP9 pour afficher les plateaux ainsi que les chemins trouvés.

Voici différentes propositions d’heuristiques très classqiues et moins classiques :

def h0(node, dst):
    return math.sqrt( (node[1]-dst[1])**2 + (node[0]-dst[0])**2)

def h(node, dst):
    return abs(node[1]-dst[1])+abs(node[0]-dst[0])

def h1(node, dst):
    return (node[1]-dst[1])**2 + (node[0]-dst[0])**2

def h2(node , dst):
    return max(abs(node[1]-dst[1]),abs(node[0]-dst[0]))

def h3(node , dst):
    return abs(node[1]-dst[1])*abs(node[0]-dst[0])

def h4(node , dst):
    return 1/(1+(abs(node[1])))

def h5(node, dst):
    return 1/(1+(abs(node[1])+abs(node[0])))

def h6(node , dst):
    return 1/(1+(abs(node[0])))

Exercice : Pour chaqu’un des graphes de 1 à 4, tracer les chemins obtenus avec Dijkstra et A*, avec chacune des heuristiques.

Exercice : Pour chaque graphe, noter le nombres d’itérations, le nombre de sommets visités ainsi que la longueur des chemins trouvés, par Dijkstra et A* pour chacune des heuristiques.

• Quelle semble être la meilleure heuristique pour chacun des graphes ?

• Une des heuristiques est-elle meilleure que toutes les autres ?

Note

D’après Wikipédia :

Un algorithme de recherche qui garantit de toujours trouver le chemin le plus court à un but s’appelle « algorithme admissible ». Si A* utilise une heuristique qui ne surestime jamais la distance (ou plus généralement le coût) du but, A* peut être avéré admissible. Une heuristique qui rend A* admissible est elle-même appelée « heuristique admissible ».

On peut démontrer que A* ne considère pas plus de nœuds que tous les autres algorithmes admissibles de recherche, à condition que l’algorithme alternatif n’ait pas une évaluation heuristique plus précise. Dans ce cas, A* est l’algorithme informatique le plus efficace garantissant de trouver le chemin le plus court.

Le prochain exercice, va nous permettre d’observer ce qu’il se passe si l’on passe d’une heuristique admissible à une heuristique qui surestime systématiquement le coût pour atteindre la destination.

Exercice : Ecrire une fonction de signature Aw_star(G: dict, h: callable, src: int, dst: int, w: float)->list[int],int, int, telle que :

Aw_star(G, h, src, dst, w) = A_star(G, w * h, src, dst)

L’argument w agit ici comme un poids pour l’heuristique.

En prenant différentes valeurs pour w (prendre par exemple \(1\), \(10^4\) et \(10^5\)) observez les différents résultats obtenus avec le graphe G5 et toutes les heuristiques.

Comparer la longueur des chemins trouvés, observez qu’ils ne sont pas toujours optimaux mais que dans certaines situations ils ont nécessité beaucoup moins de traitement.

On pourra par exemple enregistrer les résultats dans un fichier csv, dont les colonnes seraient : [‘Fonctions’,’Poids w’,’Longueur’,’Sommets traités’,’Itérations’], puis ajouter une colonne pour calculer le pourcentage que représente l’augmentation de la longueur du chemin par rapport à la longueur optimale, puis trier les données seulon le nombre de sommet traités.

Quelques exemples de résultats :